SC Manual

Introduction

Realistic simulations of the operation of a complex machine like an accelerator not only require a good model of the beam dynamics, but also have to acknowledge the fact that only incomplete information about the actual machine state is available during operation, due to the many unknowns in the machine geometry, the magnetic fields and the beam-diagnostic systems. The SC toolbox addresses this issue by making clear distinctions between machine parameters that are accessible during operation and the parameters that go into the beam dynamics simulation of the machine, e.g. by implementing a transfer-function, relating magnet setpoints to the actually realized magnetic fields.

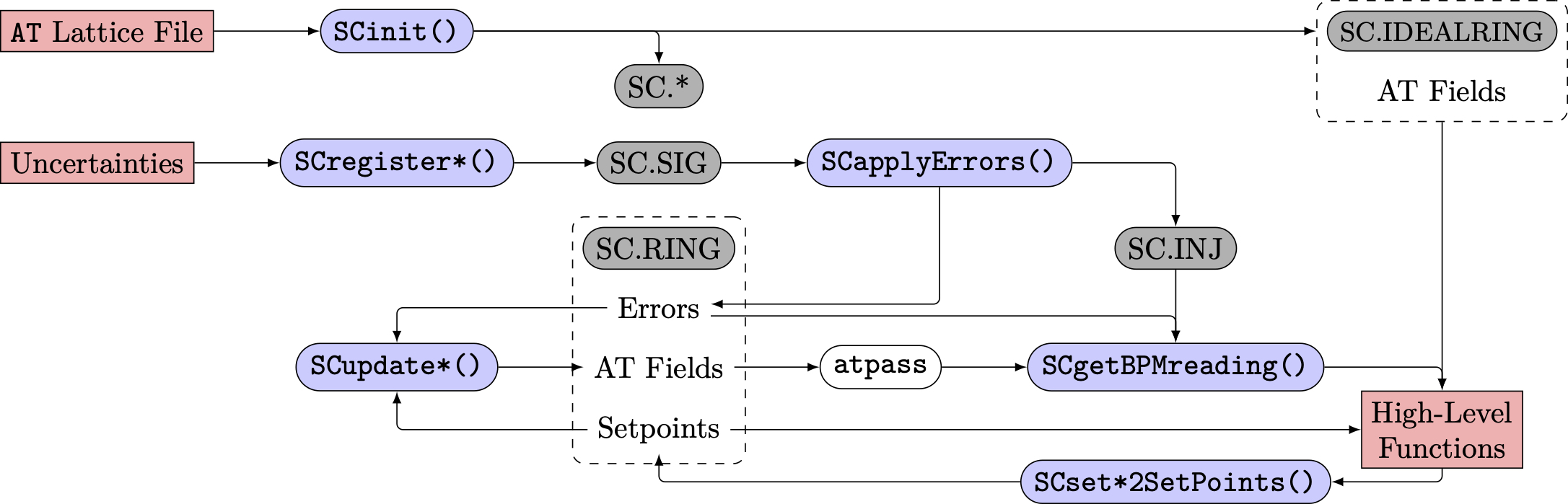
Figure 1. Schematic drawing of the workflow of the SC toolkit.

Typical usage of the SC toolbox follows the steps

Initialization of the SC core structure
Error source definition & registration of elements
Generation of a machine realization including errors
Interaction with the machine

which are described in the following. Thereafter we describe the definition of error sources, followed by a usage example for a complete correction chain and a list of all implemented functions.

Initialization

In a first step, the user initializes the toolbox by calling SCinit with the AT lattice of his or her machine as input. This sets up a matlab-structure, usually assigned the variable name SC, with which nearly all subsequent functions of the toolbox interact. Within this central structure all relevant information about the machine and the error sources is stored.

Error Source Definition & Registration

In the next step, the user registers elements like magnets, BPMs or cavities including all error sources they would like to consider in the SC structure, using the SCregister* function family. The SCregister* functions typically take the ordinates of the elements in the lattice (see SCgetOrds) and values for the uncertainties for any of the parameters used by the AT tracking code, as well as some parameters specific to SC 's error model as input.

The uncertainties are given as additional name-value pairs to the SCregister* function, while the name reflects the field name to which the error eventually should be applied. All cavities, BPMs, magnets and support structures can be registered element- or group-wise.

Element ordinates and uncertainties are centrally stored in SC.SIG and SC.ORD, respectively, and auxiliary fields in the lattice elements are initialized. Fields in SC.ORD may include

BPM: Array with all registered BPM ordinates (SCregisterBPMs)
Magnet: Array with all registered magnet ordinates (SCregisterMagnets)
Cavity: Array with all registered cavity ordinates (SCregisterCAVs)
CM: Array with all registered horizontal and vertical corrector magnets ordinates (SCregisterMagnets)
SkewQuad: Array with all registered skew quadrupole corrector magnets ordinates (SCregisterMagnets)
Girder: Array with registered girder start and end ordinates (SCregisterSupport)
Section: Array with registered section start and end ordinates (SCregisterSupport)
Plinth: Array with registered plinth start and end ordinates (SCregisterSupport)

Further, SCregister* functions are used to specify advanced properties of the elements which are subsequently accounted for by the toolbox; for instance the user here specifies which magnets are ``split''- or combined-function magnets, or which magnets should be used as a dipole or skew quadrupole correctors including their limits etc. The function SCplotLattice visualizes the lattice properties including the registration of magnets and diagnostic devices. The function SCsanityCheck helps identifying unreasonable registration of elements.

Generation of a Machine Realization

Errors are randomly generated based on the uncertainties stored in SC.SIG and applied to the lattice via SCapplyErrors. By default, errors are modeled to follow a 2 sigma-truncated Gaussian distribution, where sigma is the value specified in SC.SIG. The actual realization of misalignments can be viewed by calling SCplotSupport.

Multiple calls to SCapplyErrors produce a family of lattice realizations following the same error distribution, allowing to comfortably set up Monte-Carlo tolerance studies. See error descriptions for a detailed list of considerd error sources.

Interaction with the Machine

The operator / the control system of a particle accelerator only has incomplete information about the state of the machine and can influence the beam only indirectly. To account for this circumstance the SC toolbox implements the function SCgetBPMreading and the function family SCset*2SetPoints for CMs, cavities, and other magnets.

SCgetBPMreading models the process of injecting a bunch into the machine and observing the readings of the BPMs previously defined by SCregisterBPMs, taking into account injection errors, BPM offsets, BPM calibration errors, and more as described in the error descriptions.

All information regarding the injection pattern are centrally stored in the SC.INJ structure, which includes the fields

nParticles: Number of particles for tracking.
nTurns: Number of turns for tracking.
nShots: Number of injections used for averaging the BPM readings.
beamLostAt: Fraction of particles below which a BPM does not return a proper reading anymore but a beam loss
Z0ideal: [6 x 1] array defining the ideal injection vector.
Z0: [6 x 1] array defining the current injection vector.
beamSize: [6 x 6] array defining the beam sigma matrix.
randomInjectionZ: [6 x 1] array defining the shot-to-shot injection jitter.
trackMode: String defining the tracking mode.

Possible tracking modes are

'TBT' (turn-by-turn): A bunch is tracked for the specified number of turns and the readings of the BPMs in each individual turn are returned.
'pORB' (pseudo-orbit mode): The BPM readings are averaged over the turns, giving a good estimate of the orbit, without having actually achieved stored beam.
'ORB' (orbit mode): It is assumed that stored beam has been achieved, so that the AT function findorbit6 can be used to determine the orbit and BPM errors are applied. nTurns and nParticles are obsolete in this tracking mode

Members of the SCset*2SetPoints family model the process of assigning the set point of an experimentally accessible variable in the control system of the accelerator, for instance the strength of a quadrupole magnet. Based on these setpoints the actual simulation parameters going into the AT tracking routine are calculated by a subsequent call to, for instance, the SCupdateMagnets function. This mechanism provides a powerful layer of abstraction, which also allows to easily extend and modify the underlying error models during further development of the toolbox, without the need to modify any existing user-side code.

All commissioning routines implemented in SC exclusively use these functions to interact with the machine, so that the commissioning simulation is conducted from the point of view of a real-world operator.

Error Sources

The following will give an overview of the error sources considered in the SC toolbox.

BPMs

The BPM errors are stored in fields of the corresponding BPM lattice element and include

Noise: [1 x 2] array of horizontal and vertical turn-by-turn BPM noise.
NoiseCO: [1 x 2] array of horizontal and vertical stored beam BPM noise.
CalError: [1 x 2] array of horizontal and vertical BPM calibration errors.
Offset: [1 x 2] array of horizontal and vertical individual BPM offsets.
SupportOffset: [1 x 2] array of horizontal and vertical support structure (girder) offsets w.r.t. the design coordinate frame at the location of the BPMs.
Roll: Individual BPM rolls
SupportRoll: Support structure (girder) roll w.r.t. the design coordinate frame at the location of the BPMs.
SumError: Calibration error of the sum signal. The sum signal is used to determine the beam loss location with a cutoff as defined SC.INJ.beamLostAt (see injection pattern).

Cavities

The cavity errors are stored in fields of the corresponding cavity lattice element and include

VoltageOffset: Offset of cavity voltage w.r.t. to the voltage setpoint
VoltageCalError: Calibration error of cavity voltage w.r.t. to the voltage setpoint
FrequencyOffset: Offset of cavity frequency w.r.t. to the frequency setpoint
FrequencyCalError: Calibration error of cavity frequency w.r.t. to the frequency setpoint
TimeLagOffset: Offset of cavity time lag w.r.t. to the time lag setpoint
TimeLagCalError: Calibration error of cavity time lag w.r.t. to the time lag setpoint

The cavity fields used for tracking by AT, for example Frequency, are calculated by SCupdateCAVs considering the current setpoint FrequencySetPoint, calibration errors FrequencyCalError and offset FrequencyOffset according to

Frequency = (1 + FrequencyCalError) * FrequencySetPoint + FrequencyOffset.

Magnets

The magnet errors are stored in fields of the corresponding magnet lattice element and include

CalErrorB: [1 x N] array of calibration errors of the PolynomB fields w.r.t. the corresponding setpoints.
CalErrorA: [1 x N] array of calibration errors of the PolynomA fields w.r.t. the corresponding setpoints.
PolynomBOffset: [1 x N] array of offset errors of the PolynomB fields w.r.t. the corresponding setpoints.
PolynomAOffset: [1 x N] array of offset errors of the PolynomA fields w.r.t. the corresponding setpoints.
MagnetRoll: [1x3] array [az,ax,ay] defineing roll (around z-axis), pitch (roll around x-axis) and yaw (roll around y-axis) angle error of magnet (w.r.t. support structure).
SupportRoll: [1x3] array [az,ax,ay] defineing roll (around z-axis), pitch (roll around x-axis) and yaw (roll around y-axis) angle error of magnet support structure w.r.t. the design coordinate frame..
SupportOffset: [1 x 3] array [dx,dy,dz] of horizontal, vertical and longitudinal offset errors of magnet support structure w.r.t. the design coordinate frame.
MagnetOffset: [1 x 3] array [dx,dy,dz] of horizontal, vertical and longitudinal offset errors of magnet (w.r.t. support structure).
T1: [6 x 1] array of offsets w.r.t. the design coordinate frame which are added at to the particle coordinates at the entrance of the lattice element (standard AT field). Calculated from current magnet misalignments via SCgetTransformation.
T2: [6 x 1] array of offsets w.r.t. the design coordinate frame which are added at to the particle coordinates at the exit of the lattice element (standard AT field). Calculated from current magnet misalignments via SCgetTransformation.
R1: [6 x 6] rotation matrix w.r.t. the design coordinate frame which is multiplied with the particle coordinates at the entrance of the lattice element (standard AT field). Calculated from current magnet misalignments via SCgetTransformation.
R2: [6 x 6] rotation matrix w.r.t. the design coordinate frame which is multiplied with the particle coordinates at the exit of the lattice element (standard AT field). Calculated from current magnet misalignments via SCgetTransformation.

See SCregisterMagnets for a list of all SC related lattice element fields. The magnetic multipole components used for tracking by AT, for example PolynomB are calculated by SCupdateMagnets considering current setpoints SetPointB, calibration errors CalErrorB and field offsets PolynomBOffset according to

PolynomB = (1 + CalErrorB) .* SetPointB + PolynomBOffset.

The field offset may include a bending angle error of a pure dipole magnet or can be used to specify static (higher order) multipole errors, see below.

If the considered magnet is registered as a combined function magnet, the actual bending angle is considered to depend on the quadrupole set point. In order to capture that effect, the proper horizontal dipole field is added which results from a quadrupole set point variation from the design value. It is thereby assured that the coordinate system remains unchanged by a rotation of dipole magnets.

Higher order multipoles

Higher order multipole errors can be assigned in two different ways; static or dynamically updated. Dynamically updated multipoles are typically attributed to systematic multipoles.

Systematic multipole tables must be in AT’s PolynomA/B units and normalized to the considered component. For example, a [Nx2] table AB_HCM containing the multipoles induced by the excitation of a horizontal dipole corrector coil must have 1.0 at index AB_HCM(1,2), for a table with systematic multipoles corresponding to a skew quadrupole corrector it would be AB_SQ(2,1)=1.

Multipole error tables can be read by SCmultipolesRead from a file and set by SCsetMultipoles to the lattice structure. After setting the systematic multipoles with SCsetMultipoles the corresponding lattice element may include the fields

SysPolAFromA: {[1 x N1], [1 x N2], … [1 x Nn]} cell array containing normalized systematic PolynomA multipole errors from PolynomA entrys
SysPolAFromB: {[1 x N1], [1 x N2], … [1 x Nn]} cell array containing normalized systematic PolynomA multipole errors from PolynomB entrys
SysPolBFromA: {[1 x N1], [1 x N2], … [1 x Nn]} cell array containing normalized systematic PolynomB multipole errors from PolynomA entrys
SysPolBFromB: {[1 x N1], [1 x N2], … [1 x Nn]} cell array containing normalized systematic PolynomB multipole errors from PolynomB entrys

For the example above with a HCM and a skew quadrupole corrector coil the fields would like like the follwoing:

SysPolAFromB = {AB_HCM(:,1)}
SysPolBFromB = {AB_HCM(:,2)}
SysPolAFromA = {[], AB_SQ(:,1)}
SysPolBFromA = {[], AB_SQ(:,2)}

Note that each array of multipoles may have a different length and that SCsetMultipoles sets the corresponding primary component to zero so that it does not get added later on. Each time the magnet fields are updated via SCupdateMagnets, the systematic multipoles are scaled by the current magnet excitation. In this example the normal and skew multipole components related to the skew quadrupole excitation are calcualted as

polA_SQ(i) = [(1 + CalErrorA(2)) .* SetPointA(2)] * SysPolAFromA{2}(i),

polB_SQ(i) = [(1 + CalErrorA(2)) .* SetPointA(2)] * SysPolBFromA{2}(i),

and the normal and skew multipoles associated with the horizontal dipole excitation goes as

polA_HCM(i) = [(1 + CalErrorB(1)) .* SetPointB(1)] * SysPolAFromB{1}(i),

polB_HCM(i) = [(1 + CalErrorB(1)) .* SetPointB(1)] * SysPolBFromB{1}(i).

All systematic multipoles are calculated analogously, summed up and added to the primary coil field excitations.

Additionally random multipole errors can be assigned via SCsetMultipoles. Here each multipole table entry gets scaled with a 2-sigma truncated Gaussian random number and stored in the lattice element field PolynomBOffset and PolynomBOffset. It is hereby assumed that the random multipole errors are static and not affected by the setpoints of the magnets.

Injected beam

The injected beam errors include a random shot-to-shot variation as well as a static offset from the 6D design injection-trajectory. All errors regarding the injection pattern are centrally stored in the SC.INJ structure and include the fields

Z0: [6 x 1] array defining the current injection vector.
beamSize: [6 x 6] array defining the beam sigma matrix.
randomInjectionZ: [6 x 1] array defining the shot-to-shot injection jitter.

Each time a bunch is generated by SCgenBunches, the random injection error is calculated and added to the mean injected beam trajectory. If the number of particles per bunch is larger than one, individual particle launch conditions are randomly distributed around the bunch centroid using the beam sigma matrix with 3 sigma-truncated Gaussian distribution. Otherwise the single macro-particle per bunch is launched at the bunch centroid trajectory.

Support and Alignment

The transverse misalignment model was developed to reflect the magnet support structure of the ALS-U facility and includes the concepts of girders, plinths, and sections as illustrated in Figure 2. Support structure elements can be registered using SCregisterSupport. Girders may have offset and roll errors, while sections and plinths (the concrete slabs on which girders are mounted) are currently considered to have offset errors only.

By default it is assumed that the magnets and BPMs are mounted on girders (if registered). The offset and roll errors of BPMs and magnets are calculated by SCupdateSupport as a sum of their individual misalignment and the misalignment of the girder at the element location. This feature can be switched off in SCupdateSupport so that only random misalignment of the elements are considered. The actual misalignment distribution can be plotted using SCplotSupport.

Note that in order to apply any support structure misalignments, girders must be registered.

Figure 2. Illustration of different possible support structure implementations (see SCregisterSupport for more details and examples).

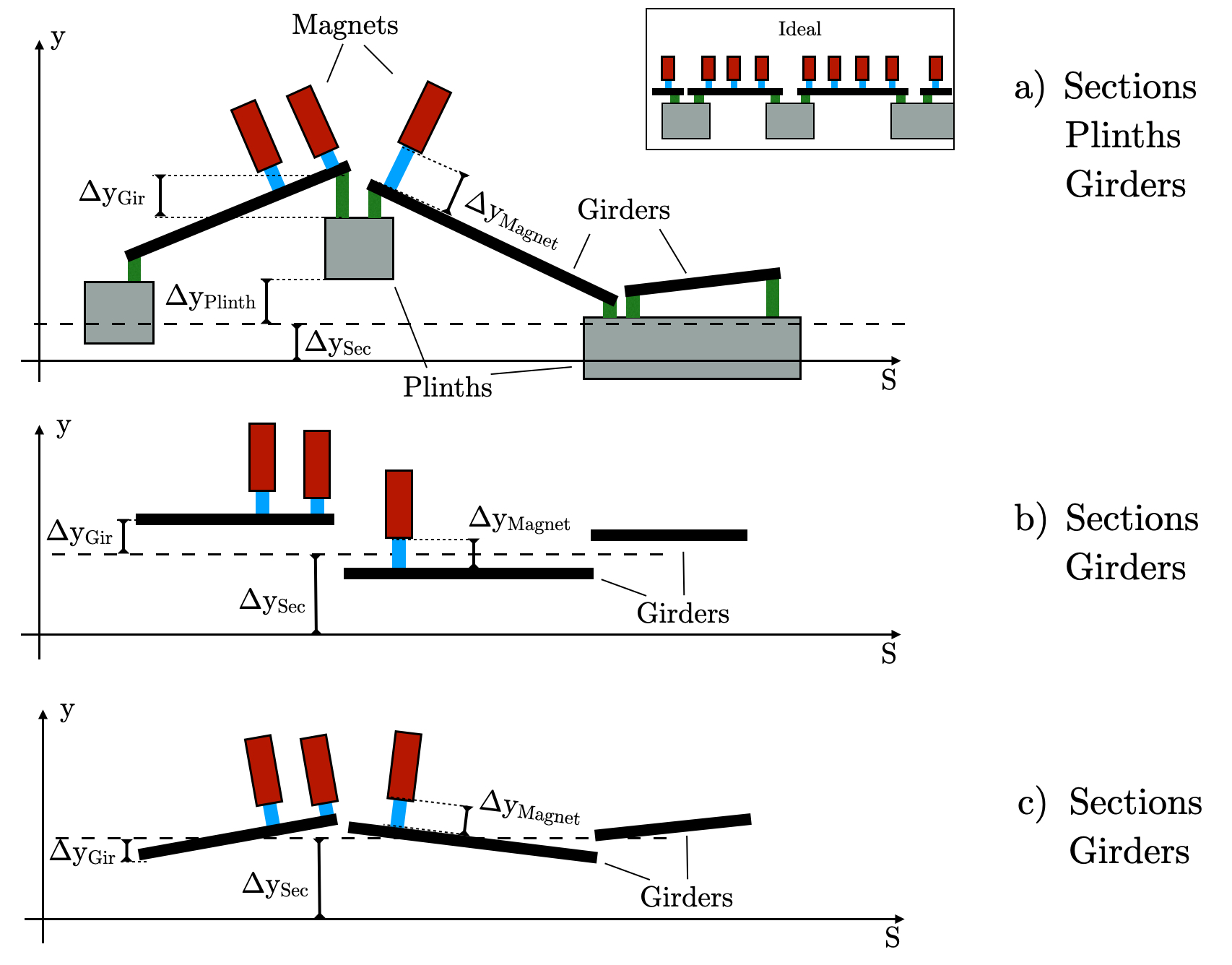
A global circumference error is modeled by SCscaleCircumference which scales all drift spaces such that the sections between two dipoles are scaled coherently.

It is worth noting that the ‘coordinate system’ of the BPMs may differ from AT’s reference system defined by the ideal lattice, as illustrated in Figure 3.

Figure 3. Illustration of the toolkit coordinate system with misalignments.

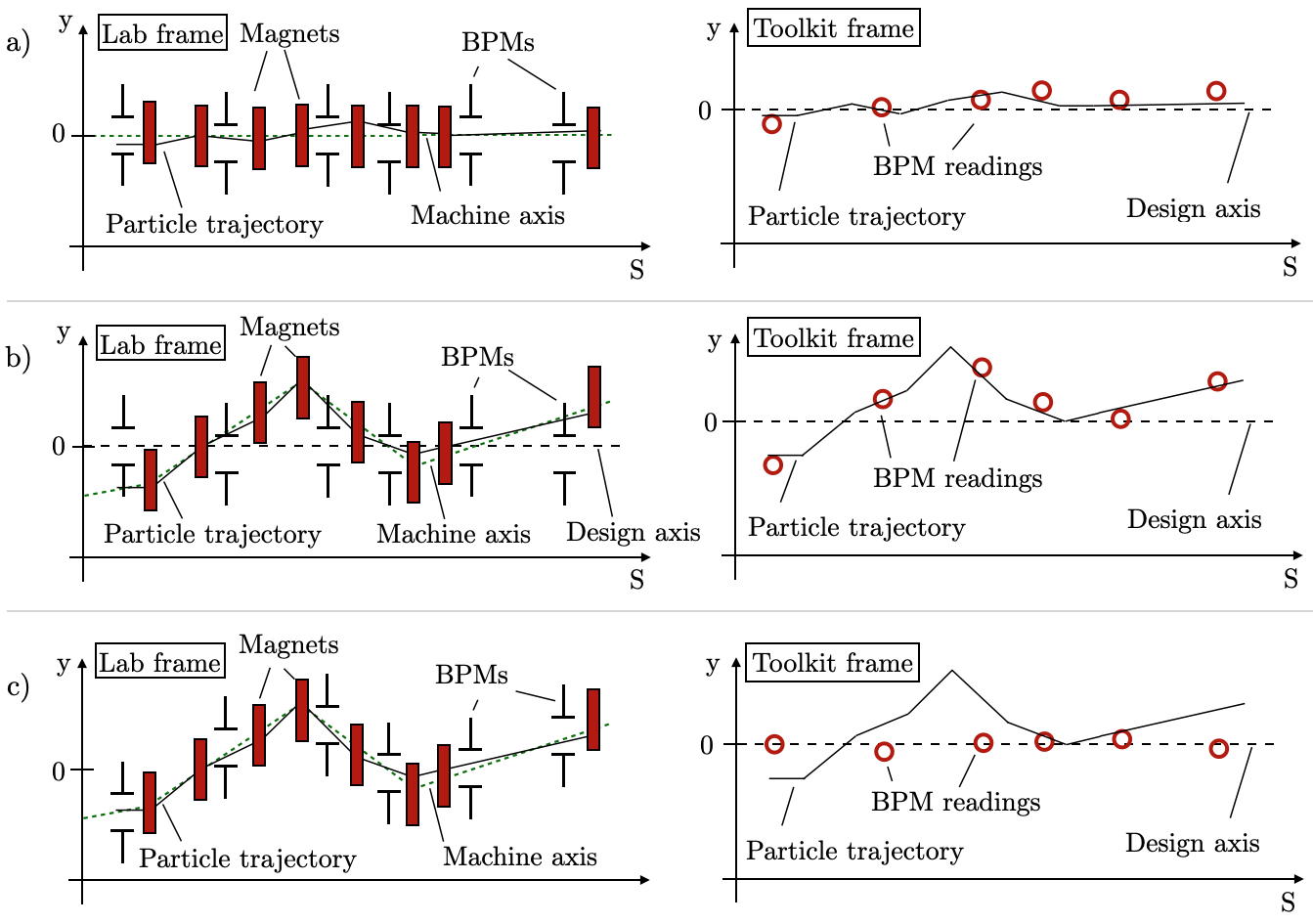
If only small random magnet and BPM errors are considered as in Figure 3 a), the particle trajectories and the BPM readings follow the design axis which is identical to the machine axis as defined by the magnet centers. In b) we assume a well corrected machine, e.g. one where the particles pass through the magnet centers which have offsets due to significant girder offsets. The BPMs in this example are distributed around the design axis. Both particle trajectories and BPM readings show large oscillations in AT’s coordinate system as the particles follow the magnets.

In the toolkit, however, it is by default assumed that BPMs are mounted on the girders, as indicated in c). While the particle trajectory oscilations remain, the calculated BPM readings in this case are distributed around AT’s design axis. In such a case using AT’s findorbit6() to calculate the closed orbit deviation would not necessarily reflect the machine state. Instead, the orbit deviation with respect to the magnet centers should be evaluated, see SCgetCOD.

SC Usage Example - FODO Lattice

In this example we present a complete simulated commissioning correction chain using a FODO lattice. The matlab script can be downloaded here.

Setup enviroment

Clear workspace, initialize the global variable plotFunctionFlag.

clear all
global plotFunctionFlag

Set path to the AT function atpath and let AT set it’s paths. Also set the path to the MML LOCO implementation and to the main SC folder which contains e.g. the function SCinit.

addpath('~/at/atmat');
atpath()
addpath('~/MML/applications/loco/');
addpath('~/sc');

Define lattice file

Define a simple FODO lattice and print the summary.

QF   = atquadrupole('QF',...
	0.5, 1.2,...
	'PassMethod','StrMPoleSymplectic4RadPass',...
	'Energy',2.5E9);
QD   = atquadrupole('QD',...
	0.5,-1.2,...
	'PassMethod','StrMPoleSymplectic4RadPass',...
	'Energy',2.5E9);
SF   = atsextupole('SF',...
	0.1, 6.0487,...
	'PassMethod','StrMPoleSymplectic4RadPass',...
	'Energy',2.5E9);
SD   = atsextupole('SD',...
	0.1,-9.5203,...
	'PassMethod','StrMPoleSymplectic4RadPass',...
	'Energy',2.5E9);
BEND = atsbend('BEND',...
	1,2*pi/40,...
	'PassMethod','BndMPoleSymplectic4Pass',...
	'Energy',2.5E9);
RFC  = atrfcavity('RFCav','Energy',2.5E9);
D2   = atdrift('Drift',0.25);
D3   = atdrift('Drift',0.2);
MARK = @(name) atmarker(name,'IdentityPass');

cell = [{D2};{MARK('SectionStart')};...
	{MARK('GirderStart')};{BEND};{D3};{SF};{D3};{MARK('GirderEnd')};...
	{MARK('GirderStart')};{MARK('BPM')};{QF};{D2};{D2};{BEND};{D3};{SD};...
	{D3};{QD};{D2};{MARK('BPM')};{MARK('GirderEnd')};{MARK('SectionEnd')}];

RING = [{RFC};repmat(cell,20,1)];
RING = atsetcavity(RING,20e5,1,50);

atsummary(RING);

Initialize toolbox

Initialize the SC toolbox with the previously defined lattice cell structure.

SC = SCinit(RING);

Register lattice in SC

In the following section all relevant elements and error sources are registered in SC.

Identify all BPMs in lattice structure and register them including uncertainties of the calibration factor, offset, roll, turn-by-turn noise and stored beam noise.

ords = SCgetOrds(SC.RING,'BPM');
SC = SCregisterBPMs(SC,ords,...
	'CalError',5E-2 * [1 1],... % x and y, relative
	'Offset',500E-6 * [1 1],... % x and y, [m]
	'Noise',10E-6 * [1 1],...   % x and y, [m]
	'NoiseCO',1E-6 * [1 1],...  % x and y, [m]
	'Roll',1E-3);               % az, [rad]

Identify the QFs in the lattice structure and register them as horizontal corrector magnets with a limit of 1mrad and include uncertainties of the CM calibration factor, quadrupole strength error, magnet offset and magnet roll.

ords = SCgetOrds(SC.RING,'QF');
SC = SCregisterMagnets(SC,ords,...
	'HCM',1E-3,...                      % [rad]
	'CalErrorB',[5E-2 1E-3],...         % relative
	'MagnetOffset',200E-6 * [1 1 0],... % x, y and z, [m]
	'MagnetRoll',200E-6* [1 0 0]);      % az, ax and ay, [rad]

Identify the QDs in the lattice structure and register them as vertical corrector magnets with a limit of 1mrad and include uncertainties of the CM calibration factor , quadrupole strength error, magnet offset and magnet roll.

ords = SCgetOrds(SC.RING,'QD');
SC = SCregisterMagnets(SC,ords,...
	'VCM',1E-3,...                      % [rad]
	'CalErrorA',[5E-2 0],...            % relative
	'CalErrorB',[0 1E-3],...            % relative
	'MagnetOffset',200E-6 * [1 1 0],... % x, y and z, [m]
	'MagnetRoll',200E-6* [1 0 0]);      % az, ax and ay, [rad]

Identify the BENDs in the lattice structure and register them with a relative bending angle error and magnet offset and magnet roll.

ords = SCgetOrds(SC.RING,'BEND');
SC = SCregisterMagnets(SC,ords,...
	'BendingAngle',1E-3,...             % relative
	'MagnetOffset',200E-6 * [1 1 0],... % x, y and z, [m]
	'MagnetRoll',200E-6* [1 0 0]);      % az, ax and ay, [rad]

Identify the SF&SD in the lattice structure and register them as skew quadrupole corrector magnets with a K value limit of 0.1 and include uncertainties of the skew quad calibration factor, sextupole strength error, magnet offset and magnet roll.

ords = SCgetOrds(SC.RING,'SF|SD');
SC = SCregisterMagnets(SC,ords,...
	'SkewQuad',0.1,...                   % [1/m]
	'CalErrorA',[0 1E-3 0],...           % relative
	'CalErrorB',[0 0 1E-3],...           % relative
	'MagnetOffset',200E-6 * [1 1 0 ],... % x, y and z, [m]
	'MagnetRoll',200E-6* [1 0 0]);       % az, ax and ay, [rad]

%Identify the cavity in the lattice structure and register it including %uncertainties for the frequency [Hz], voltage [V] and phase offset [m]

ords = findcells(SC.RING,'Frequency');
SC = SCregisterCAVs(SC,ords,...
	'FrequencyOffset',5E3,... % [Hz]
	'VoltageOffset',5E3,...   % [V]
	'TimeLagOffset',0.5);     % [m]

Identify girder start and end ordinates in lattice structure and register them including uncertainties for the offset in x, y and z [m] and roll [rad]

ords = [SCgetOrds(SC.RING,'GirderStart');SCgetOrds(SC.RING,'GirderEnd')];
SC = SCregisterSupport(SC,...
	'Girder',ords,...
	'Offset',100E-6 * [1 1 0],... % x, y and z, [m]
	'Roll',200E-6* [1 0 0]);      % az, ax and ay, [rad]

Identify section start and end ordinates in lattice structure and register them including uncertainties for the offset in x, y and z [m]

ords = [SCgetOrds(SC.RING,'SectionStart');SCgetOrds(SC.RING,'SectionEnd')];
SC = SCregisterSupport(SC,...
	'Section',ords,...
	'Offset',100E-6 * [1 1 0]); % x, y and z, [m]

As a last registration step we define the 6x6 beam sigma matrix, random shot-to-shot injection variation and the uncertainty of the systematic injection errors, both in 6D. We furthermore define the relative circumference uncertainty and the percentage of partcles which can be lost while still getting a proper BPM reading.

SC.INJ.beamSize = diag([200E-6, 100E-6, 100E-6, 50E-6, 1E-3, 1E-4].^2);

SC.SIG.randomInjectionZ = [1E-4; 1E-5; 1E-4; 1E-5; 1E-4; 1E-4]; % [m; rad; m; rad; rel.; m]
SC.SIG.staticInjectionZ = [1E-3; 1E-4; 1E-3; 1E-4; 1E-3; 1E-3]; % [m; rad; m; rad; rel.; m]

SC.SIG.Circumference = 2E-4; % relative
SC.BPM.beamLostAt    = 0.6;  % relative

Define lattice apertures

In this section a simple aperture model is defined. The aperture radius of all drift spaces is 13mm, while an circular aperture is implemented in all magnets with a radius of 10mm. In order to create a pinhole, the 50th magnet is randomly choosen to get a small eliptical aperture.

for ord=SCgetOrds(SC.RING,'Drift')
	SC.RING{ord}.EApertures = 13E-3 * [1 1]; % [m]
end

for ord=SCgetOrds(SC.RING,'QF|QD|BEND|SF|SD')
	SC.RING{ord}.EApertures = 10E-3 * [1 1]; % [m]
end

SC.RING{SC.ORD.Magnet(50)}.EApertures = [6E-3 3E-3]; % [m]

Check registration

In this section the SC registration is checked for consistency and the lattice is plotted.

SCsanityCheck(SC);

SCplotLattice(SC,'nSectors',10);

Apply errors

The next step is to generate and apply an error set based on the previolusly defined uncertainties. The misalignments are plotted.

SC = SCapplyErrors(SC);

SCplotSupport(SC);

Setup correction chain

At this point the parameters of the correction chain may be defined. In this example, we switch off the cavity and the sextupole magnets. Furthermore the 1 and 2-turn model trajectory response matrices are calcualted and a Tikhonov regularization with a regularization parameter of 50 is used to calculate the pseudo inverse of both matrices..

SC.RING = SCcronoff(SC.RING,'cavityoff');

sextOrds = SCgetOrds(SC.RING,'SF|SD');
SC = SCsetMags2SetPoints(SC,sextOrds,2,3,0,...
	'method','abs');

RM1 = SCgetModelRM(SC,SC.ORD.BPM,SC.ORD.CM,'nTurns',1);
RM2 = SCgetModelRM(SC,SC.ORD.BPM,SC.ORD.CM,'nTurns',2);

Minv1 = SCgetPinv(RM1,'alpha',50);
Minv2 = SCgetPinv(RM2,'alpha',50);

Next, we define the number of particles per bunch, shots for averaging the BPM reading and number of turns and ensure turn-by-turn tracking mode. The noise level eps defines a stopping criteria for the feedback. Finally, we switch on the global plot falg and plot uncorrected beam trajectory.

SC.INJ.nParticles = 1;
SC.INJ.nTurns     = 1;
SC.INJ.nShots     = 1;
SC.INJ.trackMode  = 'TBT';

eps   = 1E-4; % Noise level

plotFunctionFlag = 0;

SCgetBPMreading(SC);

Start correction chain

Run first turn feedback and apply correction if no error occured.

[CUR,ERROR] = SCfeedbackFirstTurn(SC,Minv1,'verbose',1);
if ~ERROR; SC=CUR; else; return; end

Switch in 2-turn mode and get full 2-turn transmission by correcting the first three BPMs of the second turn to the corresponding readings in the first turn.

SC.INJ.nTurns = 2;

[CUR,ERROR] = SCfeedbackStitch(SC,Minv2,...
	'nBPMs',3,...
	'maxsteps',20,...
	'verbose',1);
if ~ERROR; SC=CUR; else; return; end

Run trajectory feedback on 2-turn readings. Then create a period 1 orbit by matching the second turn BPM readings to the first turn.

[CUR,ERROR] = SCfeedbackRun(SC,Minv2,...
	'target',300E-6,...
	'maxsteps',30,...
	'eps',eps,...
	'verbose',1);
if ~ERROR; SC=CUR; else; return; end

[CUR,ERROR] = SCfeedbackBalance(SC,Minv2,...
	'maxsteps',32,...
	'eps',eps,...
	'verbose',1);
if ~ERROR; SC=CUR; else; return; end

In the following loop the sextupole magnets are ramped up in 5 steps and feedback is applied after each step.

for S = linspace(0.1,1,5)

	SC = SCsetMags2SetPoints(SC,sextOrds,2,3,S,...
		'method','rel');

	[CUR,ERROR] = SCfeedbackBalance(SC,Minv2,...
		'maxsteps',10,...
		'eps',eps,...
		'verbose',1);

	if ~ERROR; SC=CUR; end
end

Switch off plotting every beam, switch the cavity on and plot initial phase space.

plotFunctionFlag = 0;

SC.RING = SCcronoff(SC.RING,'cavityon');

SCplotPhaseSpace(SC,...
	'nParticles',10,...
	'nTurns',100);

The following block performs an rf phase and frequency correction in a loop and applies the corresponding correction step if no error occured.

for nIter=1:2
	% Perform RF phase correction.
	[deltaPhi,ERROR] = SCsynchPhaseCorrection(SC,...
		'nTurns',5,...      % Number of turns
		'nSteps',25,...     % Number of phase steps
		'plotResults',1,... % Final results are plotted
		'verbose',1);       % Print results
	if ERROR; error('Phase correction crashed');end

	% Apply phase correction
	SC = SCsetCavs2SetPoints(SC,SC.ORD.Cavity,...
			'TimeLag',deltaPhi,...
			'add');

	% Perform RF frequency correction.
	[deltaF,ERROR] = SCsynchEnergyCorrection(SC,...
		'range',40E3*[-1 1],... % Frequency range [kHz]
		'nTurns',20,...         % Number of turns
		'nSteps',15,...         % Number of frequency steps
		'plotResults',1,...     % Final results are plotted
		'verbose',1);           % Print results

	% Apply frequency correction
	if ~ERROR; SC = SCsetCavs2SetPoints(SC,SC.ORD.Cavity,...
			'Frequency',deltaF,...
			'add');
	else; return; end
end

Plot final phase space and check if beam capture is achieved.

SCplotPhaseSpace(SC,'nParticles',10,'nTurns',1000);

[maxTurns,lostCount,ERROR] = SCgetBeamTransmission(SC,...
	'nParticles',100,...
	'nTurns',10,...
	'verbose',true);
if ERROR;return;end

Beam capture achieved, switch to orbit mode for tracking. Calculate the orbit response matrix and the dispersion. Assume a beam based alignment procedure reduces the BPM offsets to 50um rms w.r.t. their neighbouring QF/QD magnets.

SC.INJ.trackMode = 'ORB';

MCO = SCgetModelRM(SC,SC.ORD.BPM,SC.ORD.CM,'trackMode','ORB');
eta = SCgetModelDispersion(SC,SC.ORD.BPM,SC.ORD.Cavity);

quadOrds = repmat(SCgetOrds(SC.RING,'QF|QD'),2,1);
BPMords  = repmat(SC.ORD.BPM,2,1);
SC       = SCpseudoBBA(SC,BPMords,quadOrds,50E-6);

Run orbit feedback in a loop with decreasing Tikhonov regularization parameter alpha until no further improvment is achieved. Dispersion [m/Hz] is included and scaled by a factor of 1E8 to get the same magnitude as the orbit response [m/rad] matrix.

for	alpha = 10:-1:1
	% Get pseudo inverse
	MinvCO = SCgetPinv([MCO 1E8*eta],'alpha',alpha);

	% Run feedback
	[CUR,ERROR] = SCfeedbackRun(SC,MinvCO,...
		'target',0,...
		'maxsteps',50,...
		'scaleDisp',1E8,...
		'verbose',1);
	if ERROR;break;end

	% Calculate intial and final rms BPM reading.
	B0rms = sqrt(mean(SCgetBPMreading(SC ).^2,2));
	Brms  = sqrt(mean(SCgetBPMreading(CUR).^2,2));

	% Break if orbit feedback did not result in a smaller rms BPM reading
	if mean(B0rms)<mean(Brms);break;end

	% Accept new machine
	SC = CUR;
end

Perform LOCO based linear optics correction.

The SC-LOCO interface is performed via a set of functions which are centrally stored in a pseudo-library SClocoLib. The first step is to setup the LOCO model ('setupLOCOmodel') from SC. Optional input arguments are passed to LocoFlags. In this example dispersion is included in the evaluation and the horizontal and vertical weights are set to 100. The next function ('getBPMCMstructure') sets up the BPM and CM data structures. Again, optional arguments are passed to the corresponding structure, which allows to fit the CM and BPM calibration errros. Next, the orbit response matrix and the dispersion is measured ('getMeasurment') using CM steps of 0.1mrad and an rf step of 1kHz, respectively. Finally the LOCO fit parameter structure is setup via 'setupFitparameters'. We start with all QF and QD quadrupoles which are individually powered and a strength variation of 1E-3 and 1E-4 is used to calculate the derivatives, respectively.

CMstep = 1E-4; % [rad]
RFstep = 1E3;  % [Hz]

[RINGdata,LOCOflags,Init] = SClocoLib('setupLOCOmodel',SC,...
	'Dispersion','Yes',...
	'HorizontalDispersionWeight',.1E2,...
	'VerticalDispersionWeight',.1E2);

[BPMData,CMData] =  SClocoLib('getBPMCMstructure',SC,CMstep,...
	{'BPM','FitGains','Yes'},...
	{'CM','FitKicks','Yes'});

LOCOmeasData =  SClocoLib('getMeasurement',SC,CMstep,RFstep,SC.ORD.BPM,SC.ORD.CM);

FitParameters = SClocoLib('setupFitparameters',SC,Init.SC.RING,RINGdata,RFstep,...
	{SCgetOrds(SC.RING,'QF'),'normal','individual',1E-3},... % {Ords, normal/skew, ind/fam, deltaK}
	{SCgetOrds(SC.RING,'QD'),'normal','individual',1E-4});   % {Ords, normal/skew, ind/fam, deltaK}

Run LOCO fit procedure in a loop and apply the lattice correction after each LOCO step, followed by an orbit correction step. After three iterations, include coupling (off-diagonal response matrix blocks) and the skew quadrupole correctors as LOCO fitparameters.

for n=1:6
	[~, BPMData, CMData, FitParameters, LOCOflags, RINGdata] = loco(LOCOmeasData,  BPMData,  CMData,  FitParameters,  LOCOflags,  RINGdata);

	SC = SClocoLib('applyLatticeCorrection',SC,FitParameters);

	SC = SClocoLib('applyOrbitCorrection',SC);

	SClocoLib('plotStatus',SC,Init,BPMData,CMData);

	if n==3
		LOCOflags.Coupling = 'Yes';

		FitParameters = SClocoLib('setupFitparameters',SC,Init.SC.RING,RINGdata,RFstep,...
			{SCgetOrds(SC.RING,'QF'),'normal','individual',1E-3},...
			{SCgetOrds(SC.RING,'QD'),'normal','individual',1E-4},...
			{SC.ORD.SkewQuad,'skew','individual',1E-3});
	end
end

Function Categories

The following provides a list of functions implemented in SC sorted according to their primary purpose.

Function List

SCBBA

NAME

SCBBA - Performs model independent beam based alignment

SYNOPSIS

[SC, errorFlags] = SCBBA(SC, BPMords, magOrds, [, options])

DESCRIPTION

Perform a model independend beam based alignment procedure using either two-turn trajectories or closed orbit bumps. In two-turn mode, for each BPM the injected beam trajectory is varied within a user defined range and the corresponding magnet is exercised on a user defined vector of setpoints. If the initial trajectory variation causes beam losses, the trajectory variation is reduced until all injected beam trajectories reach the BBA-BPM. If the final trajectory variation at the considered BBA-BPM is below a user defined threshold, a quadrupole may be exercised to change the phase advance between the injection point and the BPM (see option 'quadOrdPhaseAdvance'). In orbit mode an orbit bump is generated at each considerded BPM using orbit feedback with weighting factors on a user defined window around the BBA BPM. Finally, for each injected beam trajectory or orbit bump step the offset variation due the change in magnet strength (see option 'magOrder') is recorded at the BPMs used for measurement. A polynomial fit (see option 'fitOrder') is used to determine the center of the BBA-BPM with respect to the used magnet.

INPUTS

SC: SC base structure
BPMords: [2 x n] array of BPM ordinates
magOrds: [2 x n] array of magnet ordinates for the corresponding BPMs in BPMords

RETURN VALUES

SC: SC base structure with updated BPM offsets
errorFlags: [2 x n] array of error flags for each BPM

OPTIONS

The following options can be specified as name-value pairs:

'mode' (SC.INJ.trackMode): Orbit or two-turn trajectory mode ('TBT')
'outlierRejectionAt' (Inf): If the calculated BPM offset change is above the specified value, the measurement is discarted and the BPM offset is not updated.
'fakeMeasForFailures' (1): This option intends to mimic the operater’s ability to identify errors in the measurement procedure and adjust the fine tuning parameters for individual BPMs. After performing the measurement routine, the rms value of the difference between the BPM offsets and the magnet centers is calculated for both planes for all successful BPMs. If this flag is set to 1, all BPM offsets at which the measurement failed are artificially generated using a Gaussian distribution with two sigma cutoff with the rms value as described above.
'dipCompensation' (1): Flag specifying if dipole compensation at combined function magnets should be used in measurement. This works only if the considered magnet is equipped with a registered HCM. If so, the HCM is used to compensate the bending angle change when changing the main quadrupole coil. If this option is switched off, the HCM is not used and the 'real' quadrupole center is determined in the measurement and the BPM offset is adjusted in order to account for the difference between the real quadrupole center and its design value.
'nSteps' (10): Number of different trajectories/orbit bump steps for each magnet setting
'fitOrder' (1): Order of polynominal fitting, e.g. 1 for linear, 2 for quadratic fit.
'magOrder' (2): Order of magnet setpoint change, e.g. 2 for quadrupole, 3 for sextupole etc.
'magSPvec' ([0.95 1.05]): Strength variation of magnets. Can be either 1xN array of setpoint variations (applied to all specified magnets) or cell array of 1xN arrays with size(magSPvec)==size(magOrds) such that each magnet has it’s individual setpoint variation array.
'magSPflag' ('rel'): Specify how magnet setpoint as specified by option 'magSPvec' should be changed, e.g. relative or absolute (see SCsetMags2SetPoints).
'skewQuadrupole' (0): If true, it is assumed that a skew quadrupole is used. Thus, the BPM readings in the dimension other than the trajectory/orbit excitation is used for evaluation.
'switchOffSext' (0): Flag specifying if sextupole coil in BBA magnet should be switched off (e.g. if quadrupole trim coils are used).
'RMstruct' ([]): Structure containing pre-calculated response matrix etc. for orbit feedback (orbit mode only). If empty the relevant arrays are calculated with default parameters.
'orbBumpWindow' (5): Number of BPMs adjacent to BBA BPM (upstream and downstream) where the BPM weighting in orbit feedback is set to zero to allow for a pseudo orbit bump (orbit mode only).
'useBPMreadingsForOrbBumpRef' (0): If true the actual BPM readings will be used for the reference when generating the pseudo orbit bump (orbit mode only) instead of zeros. (See github issue #22)
'BBABPMtarget' (1E-3): Desired offset variation at BBA-BPM (BPM adjacent to magnet) which should be achieved by trajectory change or orbit bump.
'minBPMrangeAtBBABBPM' (0.5E-3): Threshold of change of offset at BBA-BPM; if below BBA evaluation is not performed.
'minBPMrangeDownstream' (100E-6): Minimum change of offset at downstream BPMs to be included in calculation.
'nXPointsNeededAtMeasBPM' (3): Number of x-positions at BBA-BPM required for linear regression at measurement BPMs.
'maxNumOfDownstreamBPMs' (length(SC.ORD.BPM)): Number downstream BPMs considered in the data evaluation (2-turn mode only).
'minSlopeForFit' (0.03): Minimum fitted slope at measurement BPMs with respect to magnet change which is still used in determining BPM center (a very small slope usually indicates an unfortunate phase advance and can significantly affect the measurement if not excluded). Only with linear fitting.
'maxStdForFittedCenters' (600E-6): If standard deviation of the fitted BPM centers as determined by all downstream BPMs exceeds this value, output will be 'nan'.
'maxTrajChangeAtInjection' ([0.9E-3 0.9E-3]): Maximum offset [m] and kick [rad] change at injection (2-turn mode only).
'quadOrdPhaseAdvance' ([]): Magnet ordinate which is used to change the phase advance between injection and BBA-BPM (2-turn mode only).
'quadStrengthPhaseAdvance' ([0.95 1.05]): Relative magnet strength variation used to change the phase advance between injection and BBA-BPM (2-turn mode only).
'plotLines' (0): If true, each injected beam and intermediate BBA results will be plotted.
'plotResults' (0): If true, final BBA results are plotted.
'verbose' (0): If true, debug information is printed.

ERROR FLAGS

The [2 x n] array of error flags specify if and why the measurement failed for each BPM and may have the following value:

(0): All good
(1): Max. range at BBA-BPM to small (see option 'minBPMrangeAtBBABBPM')
(2): Max. range at downstream BPM to small (see option 'minBPMrangeOtherBPM')
(3): Fitted magnetic centers to far spread out (see option 'maxStdForFittedCenters')
(4): All downstream BPM measurements failed
(5): Unexpected error during data evaluation
(6): Calculated BPM offset change too large (see option 'outlierRejectionAt')

SCapplyErrors

NAME

SCapplyErrors - Apply errors to lattice and diagnostic devices

SYNOPSIS

SC = SCapplyErrors(SC [, options])

INPUT

SC: The SC base structure.

DESCRIPTION

Applies errors to cavities, injection trajectory, BPMs, circumference, support structures and magnets if the corresponding uncertanties defined in SC.SIG are set. For example, for a magnet with ordinate ord every field defined in SC.SIG.Mag{ord} will be used to generate a random number using a Gaussian distribution with a cutoff (see option below) and sigma being the value of the uncertainty field. The number will be stored in the corresponding field of the lattice structure, thus SC.RING{ord}. An exeption are bending angle errors which are stored in the BendingAngleError field. See examples in the SCregister* functions for more details.

OPTIONS

The following options can be given as name/value-pairs:

'nSig' (2): Number of sigmas at which the Gaussian distribution of errors is truncated if not defined explicitly for individual uncertainties.

RETURN VALUE

SC: The SC base structure with applied errors.

SCcronoff

NAME

SCcronoff - switch cavity/radiation on/off

SYNOPSIS

RING = SCcronoff(RING, mode, …)

DESCRIPTION

Depending on mode SCcronoff switches the cavities / the radiation in RING on or off. Possible mode`s are ’radiationoff', 'radiationon', 'cavityoff', 'cavityon'. Multiple modes can be specified.

RETURN VALUE

RING: The modified base structure lattice.

EXAMPLES

Switch cavities and radiation in SC.RING off.

SC.RING = SCcronoff(SC.RING,'cavityoff','radiatonoff');

SCdynamicAperture

NAME

SCdynamicAperture - calculates the dynamic aperture of a ring

SYNOPSIS

[DAs, RMAXs, thetas] = SCdynamicAperture(RING, dE [, options])

DESCRIPTION

Calculates the dynamic aperture (i.e. the area of stable particle motion) of RING at energy dE. The general strategy is to find the maximum radii at which the particle motion is stable along a number of straight lines, leaving the origin at angles thetas. The dynamic aperture is then approximated as the area of the resulting polygon.

INPUT

RING: Lattice cell structure.
dE: Momentum deviation.

OPTIONS

The following options can be specified as name-value pairs:

'bounds' ([0,1e-3]): a 1x2 array containing a best guess for the upper and lower boundaries of the maximum radius. These inital boundaries are automatically refined in this routine, so a rough guess is good enough.
'nturns' (1000): number of turns used to determine whether a particle is stable.
'thetas' (linspace(0,2*pi,16)): angles at which the maximum radii are evaluated.
'accuracy' (1e-6): is the accuracy to which the dynamic aperture radii are determined [m].
'launchOnOrbit' (0): If true, particles are launched on closed orbit, otherwise on axis
'centerOnOrbit' (1): If true, the closed orbit is subtracted from the DA coordinates, which is advised for a corrected machine with support structure misalignments.
'useOrbit6' (0): If true, findorbit6 is used to determine the closed orbit, otherwise findorbit4
'auto' (0): if >0, this number of automatically determined sampling points is used, taking into account a presumed near-elliptical shape of the DA. In this case 'thetas' is ignored.
'plot' (0): if true, progress is plotted.
'verbose' (0): if true, debug messages are printed.

GLOBALS

runParallel: If true, a parfor loop is executed instead of a regular for loop.

RETURN VALUES

DA: Dynamic aperture in m^2.
RMAXs: Maximum radii at the evaluated thetas. length(thetas) array.
thetas: Angles at which the maximum radii were evaluated.

SCfeedbackBalance

NAME

SCfeedbackBalance - balance two-turn BPM readings

SYNOPSIS

[SC, ERROR] = SCfeedbackBalance(SC, Mplus [,options])

DESCRIPTION

Generates a period-1 closed orbit, after two-turn transmission has been achieved. This is done by iteratively applying correction steps, calculated based on the pseudo-inverse two-turn trajectory response matrix Mplus. The trajectory in the first turn is corrected towards the reference orbit R0, whereas the trajectory in the second turn is corrected towards the trajectory measured in the first turn; this approach seems to be more stable than the directly application of the two-turn TRM to the two-turn BPM readings. It converges to a state where BPM readings in both turns are very similar, indicating a period-1 closed orbit.

INPUT

SC: SC base structure.
Mplus: Pseudo-inverse trajectory-response matrix.

OPTIONS

The following options can be specified as name-value pairs:

'eps' (1e-5): break, if the coefficient of variation of the RMS BPM reading is below this value
'R0' (zeros): target orbit in the format [x_1 … x_n y_1 …y_n], where [x_i,y_i] is the target position at the i-th BPM.
'maxsteps' (10): A maximum of 'maxsteps' correction steps is performed.
'CMords' (SC.ORD.CM): List of CM ordinates to be used for correction
'BPMords' (SC.ORD.BPM): List of BPM ordinates at which the reading should be evaluated
'verbose' (0): If true, debug information is printed.

RETURN VALUES

SC: SC-structure with corrected SC.RING.
ERROR: Error value.

ERRORS

0: All fine.
1: A correction step resulted in less transmission, than before.
2: Transmission was lost during correction procedure. This is an indicator that Mplus might be unstable.
3: The feedback was unstable, when 'maxsteps' was reached.

SCfeedbackFirstTurn

NAME

SCfeedbackFirstTurn - achieves one-turn transmission

SYNOPSIS

[SC, ERROR] = SCfeedbackFirstTurn(SC, Mplus [, options])

DESCRIPTION

Achieves a first turn in SC.RING. This algorithm is based on the idea that repeated orbit corrections calculated via a suitably regularized pseudo-inverse trajectory-response matrix Mplus will drive the BPM readings and CM settings to a fixed point.

lim B_n = const. , with B = Phi(Mplus . B ), (1) n→oo n+1 n

where mapping Phi maps corrector kicks to BPM-readings. The RMS-values of both, BPM readings and CM settings, are determined by the regularization of Mplus. Successively - during the course of repeated application of (1) - more and more transmission is achieved throughout the ring, more magnets are traversed near their magnetic center (which is hopefully at least somewhere near the BPM zero-point), resulting in decreased kicks. If, however, the beam encounters a heavily displaced quadrupole magnet this approach is bound to fail as correction towards the center of the last reached BPM does no good, really. In this case the magnet has to be cleared using other means than linear algebra. In this approach the kicks of an increasing number of the last reached CMs are deterministically ``wiggled'' until transmission to the next BPM is achieved. Then, application of (1) is resumed.

INPUT

SC: SC base structure.
Mplus: Pseudo-inverse trajectory-response matrix.

OPTIONS

The following options can be specified as name-value pairs:

'maxsteps' (100): break, if this number of correction steps have been performed
'R0' (zeros): target orbit in the format [x_1 … x_n y_1 …y_n], where [x_i,y_i] is the target position at the i-th BPM.
'wiggleAfter' (20): Number of iterations without increased transmission to start wiggling.
'wiggleSteps' (64): Number of wiggle steps to perform, before incresing the number of wiggling-CMs.
'wiggleRange' ([50E-6 200E-6]): Range ([min,max] in rad) within which to wiggle the CMs.
'CMords' (SC.ORD.CM): List of CM ordinates to be used for correction
'BPMords' (SC.ORD.BPM): List of BPM ordinates at which the reading should be evaluated
'verbose' (0): If true, debug information is printed.

RETURN VALUES

SC: SC-structure with corrected SC.RING.
ERROR: Error value.

ERRORS

0: All fine.
1: 'maxsteps' was reached, without producing full transmission.
2: No BPM readings to beginn with.

SCfeedbackRun

NAME

SCfeedbackRun - iterative orbit correction

SYNOPSIS

[SC, ERROR] = SCfeedbackRun(SC, Mplus [, options])

DESCRIPTION

Iteratively applies orbit corrections using the pseudoinverse of the trajectory response matrix Mplus, until a break-condition specified by one of the 'OPTIONS' is met. The dispersion can be included, thus the rf frequency as a correction parameter. If the dispersion is to be included, Mplus has to have the size (length(SC.ORD.CM{1}) + length(SC.ORD.CM{2}) + 1) x length(SC.ORD.BPM), otherwise the size (length(SC.ORD.CM{1}) + length(SC.ORD.CM{2})) x length(SC.ORD.BPM), or correspondingly if the CM and/or BPM ordinates for the correction is explicitly given (see options below). SC.RING is assumed to be a lattice with transmission through all considered turns. This routine will also return, if transmission is lost.

INPUT

SC: SC base structure.
Mplus: Pseudo-inverse trajectory/orbit response matrix.

OPTIONS

The following options can be specified as name-value pairs:

'target' (0): break, if the RMS BPM reading reaches this value
'maxsteps' (30): break, if this number of correction steps have been performed
'eps' (1e-5): break, if the coefficient of variation of the RMS BPM reading is below this value
'R0' (zeros(size(Mplus,2),1)): target orbit in the format [x_1 … x_n y_1 …y_n], where [x_i,y_i] is the target position at the i-th BPM.
'scaleDisp' (0): Scaling factor for and flag indicating if the dispersion is included in the response matrix
'CMords' (SC.ORD.CM): List of CM ordinates to be used for correction
'BPMords' (SC.ORD.BPM): List of BPM ordinates at which the reading should be evaluated
'weight' (ones(size(Mplus,2),1)): weighting vector to be used in the CM step calculation in the format [x_1 … x_n y_1 …y_n], where [x_i,y_i] is the weight at the i-th BPM.
'verbose' (0): If true, debug information is printed.

RETURN VALUES

SC: SC-structure with corrected SC.RING.
ERROR: Error value.

ERRORS

0: All fine.
1: The feedback was unstable, when 'maxsteps' was reached.
2: Transmission was lost during correction procedure. This is an indicator that Mplus might be unstable.

EXAMPLES

Switch to orbit mode, get the model response matrix and dispersion. Calculate the psudo-inverse while scaling the dispersion by 1E7 and using a Tikhonov regularization parameter of 10. Finally, apply and apply orbit feedback including dispersion.

SC.INJ.trackMode = 'ORB';
MCO = SCgetModelRM(SC,SC.ORD.BPM,SC.ORD.CM,'trackMode','ORB');
eta = SCgetModelDispersion(SC,SC.ORD.BPM,SC.ORD.Cavity);
MinvCO = SCgetPinv([MCO 1E7*eta],'alpha',10);
[CUR,ERROR] = SCfeedbackRun(SC,MinvCO,'scaleDisp',1E7);

SCfeedbackStitch

NAME

SCfeedbackStitch - achieves 2-turn transmission

SYNOPSIS

[SC, ERROR] = SCfeedbackStitch(SC, Mplus [, options])

DESCRIPTION

The purpose of this function is to go from 1-turn transmission to 2-turn transmission. This is done by applying orbit correction based on the pseudo inverse trajectory response matrix 'Mplus' applied to the first BPMs in the 'SC.RING'. The reading of the BPMs in the second turn is corrected towards the reading of these BPMs in the first turn. This approach has been seen to be more stable than the direct application of the two-turn inverse response matrix to the two-turn BPM data.

INPUT

SC: SC base structure.
Mplus: Pseudo-inverse trajectory-response matrix.

OPTIONS

The following options can be specified as name-value pairs:

'nBPMs' (4): number of BPMs which are used in the second turn
'maxsteps' (30): break, if this number of correction steps have been performed
'R0' (zeros): target orbit in the format [x_1 … x_n y_1 …y_n], where [x_i,y_i] is the target position at the i-th BPM.
'nRepro' (3): Number of consecutive beam injections for which the target should be reached
'CMords' (SC.ORD.CM): List of CM ordinates to be used for correction
'BPMords' (SC.ORD.BPM): List of BPM ordinates at which the reading should be evaluated
'verbose' (0): If true, debug information is printed.

RETURN VALUES

SC: SC-structure with corrected SC.RING.
ERROR: Error value.

ERRORS

0: All fine.
1: maxsteps was reached, without producing two-turn transmission.

EXAMPLES

Calculate the 2-turn response matrix and get the pseudo inverse using a Tikhonov regularization parameter of 10. Switch the injection pattern to 2 turns and apply the stitching using the first three BPMs, a maximum of 20 steps and print debug information.

RM2 = SCgetModelRM(SC,SC.ORD.BPM,SC.ORD.CM,'nTurns',2);
Minv2 = SCgetPinv(RM2,'alpha',10);
SC.INJ.nTurns = 2;
[CUR,ERROR] = SCfeedbackStitch( SC,Minv2,'nBPMs',3,'maxsteps',20,'verbose',1);

SCfitInjectionZ

NAME

SCfitInjectionZ - Fits the injected beam trajectory

SYNOPSIS

[deltaZ0, ERROR] = SCfitInjectionZ(SC, mode [, options])

DESCRIPTION

This function calculates an transverse injection correction based on the BPM readings. Depending on the specified mode different approaches are being used. In

INPUTS

SC: SC base structure.
mode: Method to identify the injection offset. Possible are
- 'fitTrajectory': Based on the ideal lattice a trajectory is fitted which best matches the first N BPM readings as defined in the options.
- 'injectionDrift': It is assumed that a 1-turn period orbit is established (see SCfeedbackBalance) and that between the last BPM of the first turn and the first BPM in the second turn is a drift space. A linear regression is used to identify the injected beam trajectory.

OPTIONS

The following options can be specified as name-value pairs:

'nDims' (1:2): Which transverse planes should be considered.
'nBPMs' (1:3): Which BPMs.
'plotFlag' (0): If true, results are plotted.
'verbose' (0): If true, additional information is printed.

RETURN VALUE

deltaZ0: Injected beam trajectory correction.
ERROR: Error flag.

SCgenBunches

NAME

SCgenBunches - Generate injected beam particle coordinates.

SYNOPSIS

Z = SCgenBunches(SC)

DESCRIPTION

Generates bunches according to the current injection setup as defined in SC.INJ. The injection setup includes the fields:

nParticles: Number of particles for tracking.
nTurns: Number of turns for tracking.
nShots: Number of injections used for averaging the BPM readings.
Z0ideal: [6 x 1] array defining the ideal injection vector.
Z0: [6 x 1] array defining the current injection vector.
beamSize: [6 x 6] array defining the beam sigma matrix.
randomInjectionZ: [6 x 1] array defining the shot-to-shot injection jitter.
trackMode: String defining the tracking mode.

For each bunch the random injection error is calculated and added to the mean injected beam trajectory. If the number of particles per bunch is larger than one, individual particle launch conditions are randomly distributed around the bunch centroid using the beam sigma matrix. Otherwise the single macro-particle per bunch is launched at the bunch centroid trajectory. The global injection count SCinjections is increased appropriately. If a post-injection function is defined in SC.INJ.postFun, it is applied on the generated particles.

INPUTS

SC: SC base structure

RETURN VALUES

Z: [6 x (#Bunches x #Shots x #Particles)] array of injected beam particle coordinates

NAME

SCgetBPMreading - Calculates BPM readings based on the current injection scheme.

SYNOPSIS

[B, T] = SCgetBPMreading(SC [, options])

DESCRIPTION

This function calculates the particle trajectories based on the current injection setup as defined in SC.INJ and calculates the corresponding BPM readings. The injection setup is a structure with the fields:

nParticles: Number of particles for tracking.
nTurns: Number of turns for tracking.
nShots: Number of injections used for averaging the BPM readings.
Z0ideal: [6 x 1] array defining the ideal injection vector.
Z0: [6 x 1] array defining the current injection vector.
beamSize: [6 x 6] array defining the beam sigma matrix.
randomInjectionZ: [6 x 1] array defining the shot-to-shot injection jitter.
trackMode: String defining the tracking mode. If set to orbit mode ('ORB'), the AT function findorbit6 is used to calculate the trajectories. Otherwise, bunches are generated and tracking is performed. In both cases the corresponding BPM readings are calculated. If the tracking mode is 'pORB', the pseudo-orbit is calculated by averaging the turn-by-turn BPM readings.

If the global variable plotFunctionFlag is 1, the tracking results are plotted.

INPUTS

SC: SC base structure

OPTIONS

The following options can be given as name/value-pairs:

'BPMords' (SC.ORD.BPM): List of BPM ordinates at which the reading should be returned

RETURN VALUES

B: BPM readings
T: Particle trajectories

GLOBALS

plotFunctionFlag: If true, each BPM reading is plotted
isExp: Specify if a real machine is being used, so that a custom user defined function is being called instead

EXAMPLES

Switch on plotting, track 100 particles for 2 turns and store the BPM readings in B.

global plotFunctionFlag
plotFunctionFlag  = 1;
SC.INJ.trackMode  = 'TBT';
SC.INJ.nParticles = 100;
SC.INJ.nTurns     = 2;
B = SCgetBPMreading(SC);

SCgetBeamTransmission

NAME

SCgetBeamTransmission - Calculate turn-by-turn beam transmission

SYNOPSIS

[maxTurns, lostCount, ERROR] = SCgetBeamTransmission(SC [, options])

DESCRIPTION

Calculates the turn-by-turn beam transmission. A bunch is generated according to the injection setting and tracking is performed. At each turn the relative amount of lost particles is calculated. The number of survived turns is determined by using the user specified field SC.INJ.beamLostAt.

OPTIONS

The following options can be given as name/value-pairs:

'nParticles' (SC.INJ.nParticles): Number of particles.
'nTurns' (SC.INJ.nTurns): Number of turns.
'plotFlag' (0): If true, particle lost count is plotted.
'verbose' (0): If true, additional information is printed.

RETURN VALUE

maxTurns: Number of achieved turns.
lostCount: Turn-by-turn particle losses.
ERROR: False if beam survives all turns.

SCgetCMSetPoints

NAME

SCgetCMSetPoints - Return current CM setpoints

SYNOPSIS

setpoints = SCgetCMSetPoints(SC, CMords, nDim)

DESCRIPTION

Reads the setpoints of the CMs specified in CMords in the dimension nDim.

INPUTS

SC: SC base structure
CMords: Array of CM ordinates in the lattice structure
nDim: Integer specifying CM dimension ([1|2] → [hor|ver])

RETURN VALUES

setpoints: CM setpoints [rad]

SCgetCOD

NAME

SCgetCOD - Calculates closed orbit deviations with respect to magnet centers.

SYNOPSIS

COD = SCgetCOD(SC [, options])

DESCRIPTION

This function calculates the closed orbit deviation from the magnetic centers.

INPUTS

SC: SC base structure

OPTIONS

The following options can be given as name/value-pairs:

'ords' (SC.ORD.Magnet): List of magnet ordinates at which the orbit deviation should be evaluated.
'plot' (0): Flag indicating if closed orbit deviation should be plotted.

RETURN VALUES

COD: Orbit deviation w.r.t. magnet centers

EXAMPLES

Calculate closed orbit deviation in magnets named 'SF' and 'SD' and plot results.

COD = SCgetCOD(SC,'ords',SCgetOrds(SC.RING,'SF|SD'),'plot',1);

SCgetDispersion

NAME

SCgetDispersion - Measure dispersion by changing the rf frequency of the cavities

SYNOPSIS

eta = SCgetDispersion(SC, RFstep)

DESCRIPTION

Calculates reference BPM reading, then changes the rf frequency and gets a second BPM reading in order to calculate the dispersion.

INPUTS

SC: SC base structure
RFstep: Change of RF frequency in Hz

OPTIONS

The following options can be given as name/value-pairs:

'BPMords' (SC.ORD.BPM): List of BPM ordinates at which the dispersion should be returned
'CAVords' (SC.ORD.CAV): List of cavity ordinates with which the dispersion should be measured
'nSteps' (2): Number of RF steps (1st RF step is considered the reference). If more than 2 steps are specified, the measurement is bi-directional

RETURN VALUE

eta: Dispersion [m/Hz]

EXAMPLES

Calculate the dispersion with a 1 kHz rf frequency change.

eta = SCgetDispersion(SC,1E3);

SCgetModelDispersion

NAME

SCgetModelDispersion - Calculates the lattice dispersion based on current setpoints

SYNOPSIS

eta = SCgetModelDispersion(SC,BPMords,CAVords [, options])

DESCRIPTION

Calculates the dispersion at the ordinates BPMords by changing the frequency of the rf cavities specified in CAVords using the current magnet setpoints without any roll/alignment/calibration errors. Optionally the design lattice is used.

RETURN VALUES

eta: The dispersion given in [m/Hz].

OPTIONS

The following options can be given as name/value-pairs:

'rfStep' (1E3): Change of rf frequency [Hz]
'useIdealRing' (0): If true, the design lattice specified in SC.IDEALRING is used.

SCgetModelRING

NAME

SCgetModelRING - Returns a model lattice based on current setpoints

SYNOPSIS

RING = SCgetModelRING(SC, [, options])

DESCRIPTION

This function calculates a model lattice based on the setpoints of SC.RING. Misalignments, lattice errors and dipole fields are excluded.

RETURN VALUES

RING: The idealised RING structure

OPTIONS

The following options can be given as name/value-pairs:

'includeAperture' (0): If true, the returned model ring includes the aperture

SCgetModelRM

NAME

SCgetModelRM - determine the lattice response matrix based on current setpoints

SYNOPSIS

[RM, RING] = SCgetModelRM(SC,BPMords,CMords [, options])

DESCRIPTION

SCgetModelRM calculates the reponse matrix RM with the BPMs at the ordinates BPMords and corrector magnets at ordinates CMords using the current magnet setpoints without any roll/alignment/calibration errors. CMords is a 2-cell array containing the two lists for the horizontal and vertical CMs respectively. This routine can determine the turn-by-turn RM, as well as the orbit-RM; see option 'trackMode'.

RETURN VALUES

RM: The response matrix given in [m/rad].
RING: The idealised RING structure, which was used to determine the RM.

OPTIONS

The following options can be given as name/value-pairs:

'trackMode' ('TBT'): If TBT the turn-by-turn RM is calculated. If ORB the orbit RM is calculated, using findorbit6
'Z0' (zeros(6,1)): Initial condition for tracking. In ORB-mode this is used as the initial guess for findorbit6.
'nTurns' (1): Number of turns over which to determine the TBT-RM. Ignored if in ORB-mode.
'dkick' (1e-5): Kick [rad] to be added when numerically determining the partial derivatives.
'useIdealRing' (0): If true, the design lattice specified in SC.IDEALRING is used.

SCgetOrds

NAME

SCgetOrds - get ordinates of elements from FamName

SYNOPSIS

ords = SCgetOrds(RING, rx [, options])

DESCRIPTION

SCgetOrds produces the ordinates (indices) of elements in RING whose FamName matches the regular expression(s) rx. rx can be a single regex or a cell-array containing multiple regexes.

RETURN VALUE

ords: If rx is a single string ords is a single array; if rx is a cell-array ords is a cell-array containing the respective ordinates.

OPTIONS

The following options can be given as name/value-pairs:

'verbose' (0): If true additional information is printed.

EXAMPLES

Find all lattice elements in SC.RING beginning with QF and QD and return them in a single array ords.

ords = SCgetOrds(SC.RING,'^QF|^QD');

Find all lattice elements in SC.RING named QF and QD and return each of them in a cell array ords.

ords = SCgetOrds(SC.RING,{'^QF$','^QD$'});

SCgetPinv

NAME

SCgetPinv - Calculates the pseudo inverse of a matrix

SYNOPSIS

Minv = SCgetPinv(M [, options])

DESCRIPTION

Calculats the pseudo-inverse Minv of the input matrix M based on a singular value decomposition. Optional parameters define the number of singular values to be set to zero, a global scaling factor applied to all singular values or the Tikhonov regularization parameter.

INPUTS

M: Input matrix

OPTIONS

The following options can be given as name/value-pairs:

'N' (0): Number of singular values to be set to zero (starting from smallest value)
'damping' ([]): If not empty, all singular values are scaled by this factor
'alpha' ([]): If not empty, Tikhonov regularization is applied with regularization parameter alpha
'plot' (0): If true, initial and inverse singular value spectrum is plotted

RETURN VALUE

Minv: Pseudo-inverse of the input matrix.

EXAMPLES

Calculates the svd-based pseudo-inverse

Minv = SCgetPinv(M);

Calculates the svd-based pseudo-inverse while cutting off the last 10 singular values.

Minv = SCgetPinv(M,'N',10);

Calculates the svd-based pseudo-inverse while cutting off the last 10 singular values and using a Tikhonov regularization with regularization parameter of 10.

Minv = SCgetPinv(M,'N',10,'alpha',1);

SCgetRespMat

NAME

SCgetRespMat - Simulates the response matrix measurement

SYNOPSIS

[M, Err, Cmsteps] = SCgetRespMat(SC, Amp, BPMords, CMords [, options])

DESCRIPTION

Gets the beam based response matrix based on the current injection pattern and using the BPMs and CMs specified in BPMords and CMords, respectively. By default the response matrix is measured using a fixed initial kick amplitude Amp (see options below), which can be given either as a single value for all CMs or as a cell array with amplitudes for each CM specified in CMords.

If the applied CM setpoint was clipped because of CM limits, the measurement is repeated with the different direction, thus -Amp. If the beam transmission for any applied CM step is less then for the reference measurement, the CM step is scaled to 90% and the measurument is repeated.

Additionally, the measurement mode can be specified as fixedOffset. In this case Amp specifies the maximum BPM offset difference which should be achieved for each CM step. The CM step is iterated three times for every CM to reach the desired change of BPM readings.

INPUTS

SC: SC base structure
Amp: Amplitude of response matrix measurement step [m or rad], either single value or cell array defining the amplitude for every CM specified in CMords
BPMords: List of BPM ordinates at which the reading should be returned
CMords: List of CM ordinates at which the reading should be returned

OPTIONS

The following options can be given as name/value-pairs:

'mode' ('fixedKick'): Measurement mode, either 'fixedKick' or 'fixedOffset'
'nSteps' (2): Number of CM steps (1st CM step is considered the reference). If more than 2 steps are specified, the measurement is bi-directional
'fit' ('linear'): Fit method, either 'linear' or 'quadratic'
'verbose' (0): If true, debug information is printed.

RETURN VALUES

M: Response matrix [m/rad]
Err: Chi squared errror of RM entries [m/rad]
CMsteps: Maximum CM steps used for RM measurement [rad]

SCgetSupportOffset

NAME

SCgetSupportOffset - Calculates the combined support structure offset at a certain location

SYNOPSIS

off = SCgetSupportOffset(SC, s)

DESCRIPTION

This function evaluates the total offset of the support structures that have been defined via SCregisterSupport at the longitudinal positions s by linearly interpolating between support structure start- and endpoints (girder + sections + plinths, if registered). Note that this calculation may not provide the proper values if magnets with non-zero bending angle are within the support structure because it does not account for the rotation of the local coordinate system along the beam trajectory.

INPUTS

SC: The SC core structure.
s: Array of s-positions at which the offset is evaluated.

RETURN VALUE

off: [3,length(s)]-array containing the [dx/dy/dz] total support structure offsets at s.

SCgetSupportOffset

NAME

SCgetSupportOffset - Calculates the combined support structure offset at a certain location

SYNOPSIS

off = SCgetSupportOffset(SC, s)

DESCRIPTION

INPUTS

SC: The SC core structure.
s: Array of s-positions at which the offset is evaluated.

RETURN VALUE

off: [3,length(s)]-array containing the [dx/dy/dz] total support structure offsets at s.

SCgetSupportRoll

NAME

SCgetSupportRoll - Calculates the combined support structure roll, pitch and yaw angles at a certain location

SYNOPSIS

roll = SCgetSupportRoll(SC, s)

DESCRIPTION

This function evaluates the total roll, pitch and yaw angles of the support structures that have been defined via SCregisterSupport at the longitudinal positions s. The support structure pitch and yaw angles are calcualted from the horizontal and vertical offsets of the start end endpoints of the corresponding top layer support structure (the order is: girders→plinths→sections). The roll angle is a sum of the roll angles of all underlying support structures. Note that this calculation may not provide the proper values if magnets with non-zero bending angle are within the support structure because it does not account for the rotation of the local coordinate system along the beam trajectory.

INPUTS

SC: The SC core structure.
s: Array of s-positions at which the offset is evaluated.

RETURN VALUE

roll: [3,length(s)]-array containing the [az/ax/ay] total support structure rolls at s.

SCgetTransformation

SCinit

NAME

SCinit - Initializes the toolbox

SYNOPSIS

SC = SCinit(RING)

DESCRIPTION

This function is used to initialize the toolbox. Required input RING is an AT lattice cell structure, which is also saved as the ideal lattice in SC.IDEALRING. The global variables plotFunctionFlag and SCinjections are set to initial values.

GLOBALS

plotFunctionFlag ([]): If not empty, every call of SCgetBPMreading calls SCplotBPMreading, hence plotting particle trajectories and BPM readings.
SCinjections (0): Counts the number of injected beams. Gets increased by SCgenBunches

RETURN VALUE

SC: Base structure including the lattice structure.

SClocoLib

NAME

SClocoLib - Function library to use LOCO with SC

SYNOPSIS

varargout = SClocoLib(funName, varargin])

DESCRIPTION

SClocoLib is a function library intended to connect the workflows and data structures of the AT/MML function loco with the SC workflow. The input string funName defines the function which should be used. Additional input arguments and the return values of SClocoLib differ, depending on the called function. The following will describe each provided function in detail:

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

NAME

setupLOCOmodel - Sets up the LOCO model

SYNOPSIS

[RINGdata, LOCOflags, Init] = SClocoLib('setupLOCOmodel', SC [, options])

DESCRIPTION

This function sets up the LOCO model used by the function loco based on the SC structure. Additionally lattice properties of SC.RING are calculated by SCcalcLatticeProperties and stored together with SC in the structure Init. This is usefull for further LOCO steps.

INPUTS

SC: SC base structure.

OPTIONS

Additional arguments can be given as name-value pairs and are written as fields in LOCOflags.

RETURN VALUE

RINGdata: RING data used by locoresponsematrix.
LOCOflags: LOCO flags used by loco.
Init: Structure containing the initial SC structure and (disturbed) lattice properties.

EXAMPLES

Set up the LOCO model, include dispersion and set the horizontal and vertical dispersion weights to 100.

[RINGdata,LOCOflags,Init] = SClocoLib('setupLOCOmodel',SC,...
	'Dispersion','Yes',...
	'HorizontalDispersionWeight',.1E2,...
	'VerticalDispersionWeight',.1E2);

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

NAME

getBPMCMstructure - Sets up the BPM and CM data structure for LOCO

SYNOPSIS

[BPMData, CMData] = SClocoLib('getBPMCMstructure', SC, CMstep [, options])

DESCRIPTION

This function sets up the BPM and CM data structure used by the function loco based on the SC registration.

INPUTS

SC: SC base structure.
CMstep: CM step [rad] for locoresponsematrix.

OPTIONS

Additional arguments can be given as cell arrays of strings as type-name-value triples and are written as fields in in the BPM or CM structure (see examples) or to specify the used BPMs and CMs.

RETURN VALUE

BPMData: BPM data structure.
CMData: CM data structure.

EXAMPLES

Set up the BPM and CM data structures with a CM step of 0.1mrad and include fitting the BPM gains and CM kicks and use only every second CM and BPM in both planes.

[BPMData,CMData] =  SClocoLib('getBPMCMstructure',SC,1E-4,...
	{'BPM','FitGains','Yes'},...
	{'CM','FitKicks','Yes'},...
{'CMords',SC.ORD.CM{1}(1:2:end),SC.ORD.CM{2}(1:2:end)},...
{'BPMords',SC.ORD.BPM(1:2:end),SC.ORD.BPM(1:2:end)};

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

NAME

getMeasurement - Simulates the response matrix measurement

SYNOPSIS

LOCOmeasData = SClocoLib('getMeasurement', SC, CMstep, RFstep [, options])

DESCRIPTION

Sets up the 'measured' response matrix data structure used by loco. Optional arguments are passed to SCgetRespMat.

INPUTS

SC: SC base structure.
CMstep: CM step [rad] for SCgetRespMat.
RFstep: RF frequency step [Hz] for SCgetDispersion.

RETURN VALUE

LOCOmeasData: Data structure containing the response matrix.

EXAMPLES

Get the orbit response matrix and the dispersion measurement using CM steps of 0.1mrad and an rf frequency step of 1kHz, respectively.

LOCOmeasData =  SClocoLib('getMeasurement',SC,1E-4,1E3);

Get the orbit response matrix and the dispersion measurement using a BPM variation of 0.1mm and an rf frequency step of 1kHz, respectively and save the used CM steps.

[LOCOmeasData, CMsteps] =  SClocoLib('getMeasurement',SC,1E-4,1E3,'mode','fixedOffset');

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

NAME

setupFitparameters - Set up the LOCO fit parameter structure

SYNOPSIS

FitParameters = SClocoLib('setupFitparameters', SC, RING0, RINGdata, RFstep [, parameters])

DESCRIPTION

Sets up the fit parameter structure which shall be used by loco. Additionally the initial values of the fit parameters are stored, which is needed in order to eventually apply the lattice correction.

INPUTS

SC: SC base structure.
RING0: Initial (disturbed) lattice cell structure which was used for the response matrix measurement.
RINGdata: RING data structure.
RFstep: RF frequency step [Hz] for locoresponsematrix.

PARAMETERS

Additional arguments are given as cell arrays and specify the fit parameters. Each cell must be given as {ordinates, normal/skew, individual/family, deltaK} quadrupole, see examples.

RETURN VALUE

FitParameters: Fit parameter structure for loco.

EXAMPLES

Set up the LOCO fit parameter structure using all QF and QD normal quadrupoles (see also SCgetOrds) which are individually powered and using a strength variation of 1E-3 and 1E-4 to calculate the derivatives, respectively. The disturbed lattice RING0 is used to identify the initial setpoints of the fit parameters and an rf frequency step of 1kHz is assumed.

ordQF = SCgetOrds(SC.RING,'QF');
ordQD = SCgetOrds(SC.RING,'QD');
FitParameters = SClocoLib('setupFitparameters',SC,RING0,RINGdata,1E3,...
	{ordQF,'normal','individual',1E-3},...
	{ordQD,'normal','individual',1E-4});

Set up the LOCO fit parameter structure using all QFA normal quadrupoles which are powered as a group (one fit parameter), using a strength variation of 1E-4 to calculate the derivatives. The previously described structure Init (see 'setupLOCOmodel') is used to identify the initial setpoints of the fit parameters and an rf frequency step of 1kHz is assumed.

FitParameters = SClocoLib('setupFitparameters',SC,Init.SC.RING,RINGdata,1E3,...
	{SCgetOrds(SC.RING,'QFA'),'normal','family',1E-4},...

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

NAME

applyLatticeCorrection - Applies the LOCO lattice correction

SYNOPSIS

SC = SClocoLib('applyLatticeCorrection', SC, FitParameters)

DESCRIPTION

Applies the calculated lattice correction by adjusting the setpoints in SC.RING.

INPUTS

SC: SC base structure.
FitParameters: Fit parameter structure (calculated by loco).

OPTIONS

The following options can be given as name/value-pairs:

'dipCompensation' (1): Used for combined function quadrupoles (see SCsetMags2SetPoints). If this flag is set and if there is a horizontal CM registered in the considered magnet, the CM is used to compensate the bending angle difference if the applied quadrupole setpoints differs from the design value.
'damping' (1): Damping factor applied to each lattice correction step, e.g. 0.7 meaning that the correction is only applied with 70% of it’s calculated amplitude.

RETURN VALUE

SC: SC base structure with applied lattice correction.

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

NAME

applyDiagnosticCorrection - Applies the LOCO result to BPMs and CMs

SYNOPSIS

SC = SClocoLib('applyDiagnosticCorrection', SC, CMstep, CMData, BPMData [, options])

DESCRIPTION

Corrects the BPM and CM errors in SC by applying the LOCO fit results. If quadrupoles are used as CMs, the actual CM kick differs from the setpoint due to feed down effects. The (linear) routine used by LOCO to calculate the response matrices does not include that effect. Thus, the fitted CM calibration will differ from the actual calibration error of the CMs. This effect can be mitigated by using the optional 'CMcalOffsets'. The option 'meanToZero' helps to deal with cases where e.g. all fitted horizontal CM kicks are 2% too large while all horizontal BPM gains are 2% too low.

INPUTS

SC: SC base structure.
CMstep: CM step [rad] used in getBPMCMstructure.
BPMData: BPM data structure.
CMData: CM data structure.

OPTIONS

The following options can be given as name/value-pairs:

'CMcalOffsets' ([]): 1x2 cell aray containg the horizontal and vertical CM calibration offsets
'meanToZero' (0): If true, the fitted calibration factors are subtracted by their mean value before the correction is aplied
'outlierRemovalAt' ([]): If this option is set, any fitted calibration error above the threshold is discarded and not applied to the SC structure.

RETURN VALUE

SC: SC base structure with applied correction to BPM and CM errors.

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

NAME

applyOrbitCorrection - Applies orbit correction

SYNOPSIS

SC = SClocoLib('applyOrbitCorrection', SC [, options])

DESCRIPTION

Applies orbit feedback using SCfeedbackRun.

INPUTS

SC: SC base structure.

OPTIONS

The following options can be given as name/value-pairs:

'Minv' ([]): Pseudo inverse of the response matrix. If not given explicitly, SCgetModelRM is called and the Tikhonov regularization is used by SCgetPinv to calculate Minv.
'alpha' (50): Tikhonov regularization parameter.
'CMords' (SC.ORD.CM): CM oridnates used for orbit correction.
'BPMords' (SC.ORD.BPM): BPM oridnates used for orbit correction.
'verbose' (0): If true, debug information is printed.

RETURN VALUE

SC: SC base structure with applied orbit correction.

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

NAME

fitChromaticity - Fit chromaticity

SYNOPSIS

SC = SClocoLib('fitChromaticity', SC, sFamOrds, [, options])

DESCRIPTION

Applies a chromaticity correction using two sextupole families. The absolute initial setpoint variation wihtin one family remains unchanged. Note: this is not beam based but assumes the chromaticities can be measured reasonably well.

INPUTS

SC: SC base structure.
sFamOrds: [1x2] cell array of sextupole ordinates used for matching

OPTIONS

The following options can be given as name/value-pairs:

'targetChrom' ([]): [1x2] array of target chromaticities. If not specified, the chromaticities as calcualted from SC.IDEALRING are being used.
'InitStepSize' ([2 2]): Initial step size for fminsearch
'TolX' (1E-4): Step size tolerance used by fminsearch
'TolFun' (1E-3): Merrit function tolerance used by fminsearch
verbose (0): If true, debug information is printed.

RETURN VALUE

SC: SC base structure with corrected chromaticity.

EXAMPLES

Match the chromaticity in both planes to 1 using all magnets named 'SF' and 'SD' (see also SCgetOrds).

SC = SClocoLib('fitChromaticity',SC,SCgetOrds(SC.RING,{'SF','SD'}),[1 1]);

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

NAME

fitTune - Fit tunes

SYNOPSIS

SC = SClocoLib('fitTune', SC, qFamOrds, [, options])

DESCRIPTION

Applies a tune correction using two quadrupole families. The absolute initial setpoint variation wihtin one family, e.g. from LOCO remains unchanged. Note: this is not beam based but assumes the tunes can be measured reasonably well.

INPUTS

SC: SC base structure.
qFamOrds: [1x2] cell array of quadrupole ordinates used for matching

OPTIONS

The following options can be given as name/value-pairs:

'FitInteger' (1): Flag specifying if the integer part should be fitted as well.
'targetTune' ([]): [1x2] array of target tunes. If not specified, the tunes as calcualted from SC.IDEALRING are being used.
'TolX' (1E-4): Step size tolerance used by fminsearch
'InitStepSize' ([.01 .01]): Initial step size for fminsearch
'TolFun' (1E-3): Merrit function tolerance used by fminsearch
verbose (0): If true, debug information is printed.

RETURN VALUE

SC: SC base structure with corrected chromaticity.

EXAMPLES

Match the fractional tunes in both planes to the ideal tunes using all magnets named 'QF' and 'QD' (see also SCgetOrds).

SC = SClocoLib('fitTune',SC,SCgetOrds(SC.RING,{'QF','QD'}),'FitInteger',0);

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

NAME

plotStatus - Plots the current LOCO correction

SYNOPSIS

SClocoLib('plotStatus', SC, Init, BPMData, CMData)

DESCRIPTION

Plots the current beta beat, dispersion error and BPM and CM calibration and roll errors.

INPUTS

SC: SC base structure.
Init: Structure containing the initial SC structure and (disturbed) lattice properties.
BPMData: BPM data structure.
CMData: CM data structure.

SCmomentumAperture

NAME

SCmomentumAperture - Calculates the momentum aperture

SYNOPSIS

dbounds = SCmomentumAperture(RING, REFPTS, inibound [, options])

DESCRIPTION

Calculates the momentum aperture of RING at the given REFPTS. dbounds is a [2,length(REFPTS)]-array containing the upper and lower bounds of the local momentum aperture either the positive (default) or negative direction, depending on the sign of 'inibounds', which is an initial guess for the bounds of the momentum apeture. This is automatically refined in this routine, so a rough guess is good enough.

INPUT

RING: Lattice cell structure.
REFPTS: [1xN] array of lattice ordinates at which the MA should be calculated.
inibounds: [inner,outer] array of inner and outer bounds intial guess for the MA.

OPTIONS

The following options can be given as name/value-pairs:

'nturns' (1000): is the number of turns used to determine whether a particle is stable.
'accuracy'(1e-4): is the accuracy to which the momentum aperture is determined.
'stepsize'(1e-3): stepsize, with which the boundaries are expanded, when the critial point is not within them.
'debug' (0): if true, debug information is printed.
'plot' (0): if true, results are plotted.

GLOBALS

runParallel: If true, a parfor loop is executed instead of a regular for loop.

RETURN VALUE

dbounds: 2xlength(REFPTS) array containing the local momentum apertures bounds.

EXAMPLES

Calculates the positive MA bounds for the first 10 lattice elements of SC.RING with intial guess of [0,4E-2] over 1000 turns. Debug information is printed and the results are plotted.

dbounds = SCmomentumAperture(SC.RING,1:10,[0,4E-2],'debug',1,'plot',1);

Calculates the negative MA bounds at all SD magnets of SC.RING with the initial guess of [-5E-3,-2E-2] over 10000 turns in parallel mode.

ords = SCgetOrds(SC.RING,'SD');
global runParallel
runParallel = 1;
dbounds = SCmomentumAperture(SC.RING,ords,[-5E-3,-2E-2],'nturns',10000);

SCmultipolesRead

NAME

SCmultipolesRead - Reads multipole tables

SYNOPSIS

[AB, order, type] = SCmultipolesRead(fname)

DESCRIPTION

This functions reads multipole coefficients from the text-file fname, see below for an example. This file needs to contain all orders up to the maximum order; no gaps! Lines starting with # are ignored. Fields are delimited by tabs.

INPUT

fname: File to read.

RETURN VALUES

AB: [2,maxorder]-array containing the multipole coefficients
order, type: If the multipole table contains an exact 1.0, it is assumed this table is scaled to that coefficient. In that case order gives the n of that coefficent and type determines whether it is the normal (2) or skew (1) component.

EXAMPLE FILE

# Taken from v20r_SysMultipoles_R1.xlsx (table DIPA, AT conv)
# This is a comment.
# n	PolynomA(n)		PolynomB(n)
0	+0.000000000E+00	-1.712194700E-01
1	+0.000000000E+00	+2.997864116E+00
2	+0.000000000E+00	+1.121256852E+00
3	+0.000000000E+00	-5.000867669E+01
4	+0.000000000E+00	-4.233346976E+03
5	+0.000000000E+00	-6.454146352E+05
6	+0.000000000E+00	-4.014924846E+07
7	+0.000000000E+00	-8.862779057E+09
8	+0.000000000E+00	+2.614134332E+12
9	+0.000000000E+00	-5.382882472E+14

SCparticlesIn3D

NAME

SCparticlesIn3D - Re-order particle trajectories

DESCRIPTION

atpass gives its result in form of an 6x(NPART NELEM*NTURN) array, where NPART/NELEM/NTURN are the number of particles/elements/turns. This function takes this output and reorders it into an 3D array with dimensions 6x(NELEM*NTURN)xNPART.

INPUT

R: Output of atpass.
NPART: Number of particles in R.

RETURN

M: 3D array in with dimensions 6x(NELEM*NTURN)xNPART.

SCplotBPMreading

NAME

SCplotBPMreading - plots BPM readings and particle trajectories

SYNOPSIS

SCplotBPMreading(SC, B, T)

DESCRIPTION

SCplotBPMreading is a plotting function used by SCgetBPMreading and plots the BPM readings and particel trajectories including the aperture model. Note that the BPM readings mus include all registered BPMs and the trajectories must be evaluated at all lattice elements.

INPUTS

SC: SC base structure
B: BPM readings
T: Trajectories

SCplotCMstrengths

NAME

SCplotCMstrengths - plots the current CM setpoints

SYNOPSIS

SCplotCMstrengths(SC)

DESCRIPTION

Plots the current CM setpoints.

INPUTS

SC: SC base structure

SCplotLattice

NAME

SCplotLattice - Plots the lattice including the location of BPMs and CMs

SYNOPSIS

SCplotLattice(SC [, options])

DESCRIPTION

This function plots the lattice functions as well as the distribution of registered magnets including CMs and BPMs.

INPUTS

SC: SC base structure

OPTIONS

The following options can be given as name/value-pairs:

'transferLine' (0): If true the function 'twissline' is used to calculate the lattice functions
'sRange' ([]): Array ['sMin','sMax'] defining the plot range [m].
'oList' ([]): If 'sRange' is empty, 'oList' can be used to specify a list of ordinates at which the lattice should be plotted
'nSectors' (1): If 'oList' is empty, 'nSectors' can be used to plot only the first fraction of the lattice
'plotIdealRing' (1): Specify if 'SC.IDEALRING' should be used to plot twiss functions, otherwise 'SC.RING'.
'plotMagNames' (0): Specify if magnet names should be printed next to the magnets. Note: since Matlab is not able to find the best placement of text annotations automatically, it is likely required that the corresponding lines in the code are adjusted to the users discretion.
'fontSize' (16): Figure font size.

EXAMPLES

Plots the complete lattice for a ring

SCplotLattice(SC);

Plots the lattice from ordinate 30 to 130 for a transfer line

SCplotLattice(SC,'transferLine',1,'oList',30:120);

Plots the lattice of one arc for a twelfe-fold symmetric ring lattice

SCplotLattice(SC,'nSectors',12);

SCplotLattice

NAME

SCplotLattice - Plots the lattice including the location of BPMs and CMs

SYNOPSIS

SCplotLattice(SC [, options])

DESCRIPTION

This function plots the lattice functions as well as the distribution of registered magnets including CMs and BPMs.

INPUTS

SC: SC base structure

OPTIONS

The following options can be given as name/value-pairs:

'transferLine' (0): If true the function 'twissline' is used to calculate the lattice functions
'sRange' ([]): Array ['sMin','sMax'] defining the plot range [m].
'oList' ([]): If 'sRange' is empty, 'oList' can be used to specify a list of ordinates at which the lattice should be plotted
'nSectors' (1): If 'oList' is empty, 'nSectors' can be used to plot only the first fraction of the lattice
'plotIdealRing' (1): Specify if 'SC.IDEALRING' should be used to plot twiss functions, otherwise 'SC.RING'.
'plotMagNames' (0): Specify if magnet names should be printed next to the magnets. Note: since Matlab is not able to find the best placement of text annotations automatically, it is likely required that the corresponding lines in the code are adjusted to the users discretion.
'fontSize' (16): Figure font size.

EXAMPLES

Plots the complete lattice for a ring

SCplotLattice(SC);

Plots the lattice from ordinate 30 to 130 for a transfer line

SCplotLattice(SC,'transferLine',1,'oList',30:120);

Plots the lattice of one arc for a twelfe-fold symmetric ring lattice

SCplotLattice(SC,'nSectors',12);

SCplotPhaseSpace

NAME

SCplotPhaseSpace - Plots the turn-by-turn phase space

SYNOPSIS

SCplotPhaseSpace(SC [,options])

DESCRIPTION

Plots the horizontal, vertical and longitudinal turn-by-turn phase space for a bunch of particles as specified in the injection pattern SC.INJ. If 'RFCavityPass' is the specified cavity pass method, the slippage length per turn caused by a potential frequency error is calculated and the longitudinal coordinate is adjusted for plotting.

INPUTS

SC: SC base structure

OPTIONS

The following options can be given as name-vale pairs:

'nTurns' (SC.INJ.nTurns): Number of turns.
'nParticles' (SC.INJ.nParticles): Number of particles.
'ord' (1): Ordinate for plotting.
'plotCO' (0): Logical value defining if closed orbit should be plotted as well.
'customBunch' ([]): [6 x N] array of particle start points for phase space evaluation. If not specified a bunch is generated using SCgenBunches.

SCplotSupport

NAME

SCplotSupport - Plots the offset and rolls of magnets, the support structure and BPMs

SYNOPSIS

SCplotSupport(SC)

DESCRIPTION

This function plots the overall offsets [dx,dy,dz] and rolls [az,ax,ay] of all magnets and BPMs, as well as the individual contributions from different support structures (if registered). Please note that the apperance of the figure significanlty depends on the lattice (magnitude of errors or lattice size) and the used computer (screen size, Matlab version). The user might have to adjust plot apperance properties.

INPUTS

SC: SC base structure

OPTIONS

The following options can be given as name/value-pairs:

'fontSize' (12): Figure font size.
'shiftAxes' (0.03): Axes are reanranged for grouping. Depending on screen resolution this value may be adjusted.
'xLim' ([0 findspos(SC.RING,length(SC.RING)+1)]): Plot limits.

SCpseudoBBA

NAME

SCpseudoBBA - mimics the results of a BBA procedure

SYNOPSIS

[SC] = SCpseudoBBA(SC, BPMords, MagOrds, postBBAoffset)

DESCRIPTION

Sets the BPM offsets to values as would be achieved by performing a BBA procedure. The BPMs defined in BPMords are paired with the magnets defined in MagOrds and the BPM offsets are adjusted to match the magnet offsets with an accuracy of postBBAoffset.

INPUT

SC: SC base structure.
BPMords: [2 x N] array of BPM ordinates.
MagOrds: [2 x N] array of magnet ordinates.
postBBAoffset: [2 x N] array or single value of rms accuracy of pseudo BBA procedure [m].

OPTIONS

The following options can be specified as name-value pairs:

'sigma' (2): Cutoff (number of sigmas) for generating the final offset distribution.

RETURN VALUES

SC: SC-structure with adjusted BPM offsets.

EXAMPLES

Assuming that each QF, QD and QFA magnet is accompanied by one BPM, the following assumes a sucessful BBA routine and assigns a 50um BPM offset w.r.t. the magnet centers.

QuadOrds = repmat(SCgetOrds(SC.RING,'QF|QD|QFA'),2,1);
SC = SCpseudoBBA(SC,SC.ORD.BPM,QuadOrds,50E-6);

SCrampUpErrors

NAME

SCrampUpErrors - Ramps up errors while applying trajectory/orbit feedback

SYNOPSIS

[SC, ERROR] = SCrampUpErrors(SC [, options])

DESCRIPTION

This function may be used as a shortcut to the result of start-to-end correction chain. The input is the SC structure containing a SC.RING with already applied errors. SCrampUpErrors then ramps up these errors in steps while applying SCfeedbackRun. If ramping up fails, the number of steps is doubled and the procedure starts over until the number of steps exceeds 100.

INPUT

SC: The base structure containing SC.RING with applied errors

RETURN VALUES

SC: The base structure containing SC.RING with applied errors and a corrected orbit
ERROR: Error value.

OPTIONS

The following options can be given as name/value-pairs:

'nStepsRamp' (10): Number of steps for ramping up errors.
'alpha' (10): Regularization parameter to get the pseudo inverse of the response matrix.
'target' (0): (for feedback) break, if the RMS BPM reading reaches this value
'maxsteps' (30): (for feedback) break, if this number of correction steps have been performed
'eps' (1e-5): (for feedback) break, if the coefficient of variation of the RMS BPM reading is below this value
'verbose' (0): If true, debug information is printed.

EXAMPLES

Initialize SC with the lattice RING, apply the user defined function registerRING to register all required elements including uncertainties of the magnets, BPMs, RF, etc. In the next step the errors are applied by SCapplyErrors. Tracking is set to orbit mode and the previously applied errors are ramped up in 15 steps. If err=0, the output contains SC.RING with applied errors and a corrected closed orbit.

SC = SCinit(RING);
SC = registerRING(SC);
SC = SCapplyErrors(SC);
SC.INJ.trackMode = 'ORB';
[SC,err] = SCrampUpErrors(SC,'nStepsRamp',15);

SCrandnc

NAME

SCrandnc - Truncated Gaussian random number generator

SYNOPSIS

out = SCrandnc(c, [, options])

DESCRIPTION

Random number generator (Gaussian distribution with mean 0 and sigma of 1). This function calls the built in Matlab function randn but allows to specify a cut parameter c. Only numbers between -c and +c will be generated.

INPUTS

c: cutoff value

OPTIONS

size: Either [M, N] array defining the size of the output array or two values M, N. See examples.

RETURN VALUES

output: [M x N] array of random numbers with a Gaussian distribution

EXAMPLES

Generates a random number out between [-2,2] and with sigma=1.

out = SCrandnc(2);

Generates random numbers out between [-2,2] and with sigma=1 with size(out)=size(A).

out = SCrandnc(2,size(A));

Generates random numbers out between [-2,2] and with sigma=1 with size(out)=[1,10].

out = SCrandnc(2,1,10);

SCregisterBPMs

NAME

SCregisterBPMs - Registers BPMs in SC

SYNOPSIS

SC = SCregisterBPMs(SC,BPMords [, sigmas])

DESCRIPTION

Registers BPMs specified by BPMords in the SC structure and initializes all required fields in the lattice elements. The ordinates of all registered BPMs are stored in SC.ORD.BPM. The BPM realated fields in the lattice elements are

Noise: [1 x 2] array of hor./ver. turn-by-turn BPM noise
NoiseCO: [1 x 2] array of hor./ver. orbit BPM noise
CalError: [1 x 2] array of hor./ver. BPM calibration errors
Offset: [1 x 2] array of individual hor./ver. BPM offsets
SupportOffset: [1 x 2] array of hor./ver. BPM offsets which result from the corresponding girder offset at the location of the BPMs, see SCupdateSupport.
Roll: BPM roll around z-axis w.r.t. the support structure
SupportRoll: BPM roll around z-axis which results from the corresponding support structure roll at the location of the BPMs, see SCupdateSupport.
SumError: Calibration error of the sum signal. The sum signal is used to determine the beam loss location with a cutoff as defined SC.INJ.beamLostAt.

INPUTS

SC: SC base structure.
BPMords: BPM ordinates in the lattice structure.

UNCERTAINTIES

Additional name/vale-pairs are interpreted as uncertainties and passed to the sigma structure SC.SIG for the corresponding BPM. The function SCapplyErrors uses the fields of SC.SIG to randomly generate errors and applies them to the corresponding fields in SC.RING. By default a 2 sigma cutoff is applied. The user can specify a different cutoff by giving the uncertainty as a cell structure, e.g. {[1x2],nSig}, with nSig being the cutoff (see examples below).

RETURN VALUE

SC: The base structure containing required information of all BPMs.

EXAMPLES

Identify the ordinates of all elements named BPM and registers them as BPMs in SC

ords = SCgetOrds(SC.RING,'BPM');
SC = SCregisterBPMs(SC,ords);

Register the BPMs specified in ords in SC and set the uncertanty of the offset to 500um in both planes. A subsequent call of SCapplyErrors would generate a random BPM offset errors with sigma=500um.

SC = SCregisterBPMs(SC,ords,'Offset',500E-6*[1 1]);

Register the BPMs specified in ords in SC and set the uncertanty of the offset to 500um in both planes and a calibration error of the sum signal of 20%.

SC = SCregisterBPMs(SC,ords,'Offset',500E-6*[1 1],'SumError',0.2);

SC = SCregisterBPMs(SC,ords,'Offset',{500E-6*[1 1],3});

SCregisterCAVs

NAME

SCregisterCAVs - Register cavities in SC

SYNOPSIS

SC = SCregisterCAVs(SC,CAVords [, sigmas])

DESCRIPTION

Register cavities specified in CAVords in SC by initializing all required fields in the corresponding cavity lattice elements and storing the ordinates in SC.ORD.Cavity. The additional fields in the lattice elements are

VoltageSetPoint: Setpoint of cavity voltage
VoltageOffset: Offset of cavity voltage wrt. to the setpoint
VoltageCalError: Calibration error of cavity voltage wrt. to the setpoint
FrequencySetPoint: Setpoint of cavity frequency
FrequencyOffset: Offset of cavity frequency wrt. to the setpoint
FrequencyCalError: Calibration error of cavity frequency wrt. to the setpoint
TimeLagSetPoint: Setpoint of cavity phase (TimeLag)
TimeLagOffset: Offset of cavity phase wrt. to the setpoint
TimeLagCalError: Calibration error of cavity phase wrt. to the setpoint

INPUTS

SC: SC base structure.
CAVords: Cavity ordinates in the lattice structure.

UNCERTAINTIES

Additional name/vale-pairs are interpreted as uncertainties and passed to the sigma structure SC.SIG for the corresponding cavity. The function SCapplyErrors uses the fields of SC.SIG to randomly generate errors and applies them to the corresponding fields of the lattice element. By default a 2 sigma cutoff is applied. The user can specify a different cutoff by giving the uncertainty as a cell structure, e.g. {deltaF,nSig}, with nSig being the cutoff (see examples below).

RETURN VALUE

SC: The base structure containing required information of all cavities.

EXAMPLES

Identify the ordinates of all elements named 'CAV' and register them as cavities in SC

ords = SCgetOrds(SC.RING,'CAV');
SC = SCregisterCAVs(SC,ords);

Register the cavities specified in ords in SC and sets the uncertanty of the frequency offset to 1kHz. A subsequent call of SCapplyErrors would generate a random frequncy offset error with sigma=1kHz.

SC = SCregisterCAVs(SC,ords,'FrequencyOffset',1E3);

SC = SCregisterCAVs(SC,ords,'FrequencyOffset',{1E3,3});

Register the cavities specified in ords in SC and sets the uncertanty of the timelag offset to 0.3m. A subsequent call of SCapplyErrors would generate a random timelag offset error ('phase error') with sigma=0.3m and a 3 sigma cutoff.

SC = SCregisterCAVs(SC,ords,'TimeLagOffset',{0.3,3});

SCregisterMagnets

NAME

SCregisterMagnets - Register magnets in SC

SYNOPSIS

SC = SCregisterMagnets(SC, MAGords [, options])

DESCRIPTION

Registers magnets specified by MAGords in the SC structure and initializes all required fields in the lattice elements. The ordinates of all registered magnets are stored in SC.ORD.Magnet. The additional SC related fields in the lattice elements are

NomPolynomB: Nominal (design) PolynomB fields.
NomPolynomA: Nominal (design) PolynomA fields.
SetPointB: Setpoints for the PolynomB fields.
SetPointA: Setpoints for the PolynomA fields.
CalErrorB: Calibration error of the PolynomB fields wrt. the corresponding setpoints.
CalErrorA: Calibration error of the PolynomA fields wrt. the corresponding setpoints.
PolynomBOffset (optional): Offset error of the PolynomB fields wrt. the corresponding setpoints.
PolynomAOffset (optional): Offset error of the PolynomA fields wrt. the corresponding setpoints.
MagnetOffset: [1 x 3] array of horizontal, vertical and longitudinal magnet offsets (wrt. the support structure).
SupportOffset: [1 x 3] array of horizontal, vertical and longitudinal support structure offsets (if support structure is registered).
MagnetRoll: [1x3] array [az,ax,ay] defineing magnet roll (around z-axis), pitch (roll around x-axis) and yaw (roll around y-axis); all wrt. the support structure.
SupportRoll: [1x3] array [az,ax,ay] defineing support structure roll (around z-axis), pitch (roll around x-axis) and yaw (roll around y-axis); all wrt. the design coordinate frame (if support structure is registered).
BendingAngleError (optional): Error of the main bending field (corresponding uncertainty defined with BendingAngle).
CF (optional): Flag identifying the corresponding magnet as a combined function dipole/quadrupole.
HCM (optional): Flag identifying the corresponding magnet as a horizontal corrector magnet.
VCM (optional): Flag identifying the corresponding magnet as a vertical corrector magnet.
SkewQuad (optional): Flag identifying the corresponding magnet as a skew quadrupole corrector magnet.
MasterOf (optional): Array of ordinates to which the corresponding magnet acts as master (split magnets).

Optional input arguments can be given as name/value-pairs and are either used to specify certain magnet types or to define uncertainties (see below). If CMs or skew quadrupole correctors are specified, the ordinates are also stored in the corresponding fields SC.ORD.CM and SC.ORD.SkewQuad, respectively.

INPUTS

SC: SC base structure.
MAGords: Magnet ordinates in the lattice structure.

OPTIONS

The following options can be given as name/value-pairs:

'HCM' ([]): Magnet is identified as horizontal CM. The corresponding value is the horizontal CM limit and stored in SC.RING{MAGords}.CMlimit(1). E.g. set limit to Inf.
'VCM' ([]): Magnet is identified as vertical CM. The corresponding value is the vertical CM limit and stored in SC.RING{MAGords}.CMlimit(2). E.g. set limit to Inf.
'SkewQuad' ([]): Magnet is identified as skew quadrupole corrector. The corresponding value is the skew quadrupole limit and stored in SC.RING{MAGords}.SkewLimit. E.g. set limit to Inf.
'CF' (0): If true, the magnet is identified as a combined function dipole/quadrupole. That implies that the bending angle depends on the quadrupole setpoint. A variation from the design value will therefore result in a bending angle error which is added to the PolynomB(1) field.
'MasterOf' ([]): The magnets MAGords are identified as a split magnets each with N childs as specified in the corresponding value which must be a [N x length(MAGords)] array. The field calculation in SCupdateMagnets uses the setpoints and errors of the master magnet to calculate the child fields. The relative bending angle error of the master magnet e.g. is applied on the corresponding child bending angle appropriately. Split quadrupole magnets with different design gradients, however, can currently not be updated correctly.

UNCERTAINTIES

Every name/value-pair which is not explicitly mentioned in the options above is interpreted as an uncertainty and passed to the sigma structure SC.SIG for the corresponding magnets defined in MAGords (see examples below). The function SCapplyErrors uses the fields of SC.SIG to randomly generate errors and applies them to the corresponding fields of the lattice elements. By default, a Gaussian distribution with a cutoff at 2 sigma is applied. An alternative cutoff value can be given explicitly for each uncertainty type, see examples below.

EXAMPLES

Identify the ordinates of all elements named QF and register them in SC.

ords = SCgetOrds(SC.RING,'QF');
SC = SCregisterMagnets(SC,ords);

Register the magnets specified in ords in SC and set the uncertainty of the quadrupole component to 1E-3 and 30um horizontal and vertical offset.

SC = SCregisterMagnets(SC,ords, ...
	'CalErrorB',[0 1E-3],...
	'MagnetOffset',[30E-6 30E-6 0]);

Register the magnets specified in ords in SC and set the uncertainty of the quadrupole component to 1E-3 and 30um horizontal and vertical offset with a 3 sigma cutoff value (when applied with SCapplyErrors).

SC = SCregisterMagnets(SC,ords, ...
	'CalErrorB',[0 1E-3],...
	'MagnetOffset',{[30E-6 30E-6 0],3});

Register the magnets specified in ords in SC and set the uncertainty of the quadrupole component to 1E-3, 30um horizontal and vertical offset and 100um longitudinal offset.

SC = SCregisterMagnets(SC,ords, ...
	'CalErrorB',[0 1E-3],...
	'MagnetOffset',[30E-6 30E-6 100E-6]);

SC = SCregisterMagnets(SC,ords, ...
	'Roll',[100E-6 100E-6 100E-6]);

Register split magnets. Identify the magnets named BENDa ([1xN] array masterOrds) and the magnets named BENDb and BENDc ([2xN] array childOrds) and register the masterOrds as the master magnets of the children in the corresponding columns of childOrds. The uncertanty of the bending angle is set to 1E-4.

masterOrds = SCgetOrds(SC.RING,'BENDa');
childOrds  = [SCgetOrds(SC.RING,'BENDb');SCgetOrds(SC.RING,'BENDc')];
SC = SCregisterMagnets(SC,masterOrds, ...
	'BendingAngle',1E-4,
	'MasterOf',childOrds);

Register the magnets specified in ords in SC and set the uncertainty of the quadrupole component to 1E-3 and the uncertainty of the bending angle to 1E-4, the latter with a 3 sigma cutoff.

SC = SCregisterMagnets(SC,ords, ...
	'CalErrorB',[0 1E-3], ...
	'BendingAngle',{1E-4,3});

Register the magnets specified in ords in SC as combined function magnets and sets the uncertanty of the quadrupole component to 1E-3.

SC = SCregisterMagnets(SC,ords, ...
	'CF',1, ...
	'CalErrorB',[0 1E-3]);

Register the magnets specified in ords in SC and set the uncertanty of the skew quadrupole component to 2E-3 and the uncertanty of the sextupole component to 1E-3.

SC = SCregisterMagnets(SC,ords, ...
	'CalErrorA',[0 2E-3 0], ...
	'CalErrorB',[0 0 1E-3]);

Register the magnets specified in ords in SC as horizontal and vertical CMs, set their dipole uncertanties to 5% and 1%, respectively and define no CM limits.

SC = SCregisterMagnets(SC,ords, ...
	'HCM',Inf, ...
	'VCM',Inf, ...
	'CalErrorB',5E-2, ...
	'CalErrorA',1E-2);

Register the magnets specified in ords in SC as horizontal and vertical CMs, set their uncertanties to 5% and 1%, respectively and their limits to 1 mrad. Furthermore, set the uncertanty of the skew quadrupole component to 2E-3 and the uncertanty of the sextupole component to 1E-3.

SC = SCregisterMagnets(SC,ords, ...
	'HCM',1E-3, ...
	'VCM',1E-3, ...
	'CalErrorB',[5E-2 0 1E-3], ...
	'CalErrorA',[1E-2 2E-3 0]);

SCregisterSupport

NAME

SCregisterSupport - Register magnet support structures in SC

SYNOPSIS

SC = SCregisterSupport(SC, type, ords [, options])

DESCRIPTION

Initializes magnet support structures such as sections, plinths and girders in SC. The function input be given as name-value pairs, starting with the structure type and structure ordinates defining start- end endpoints. Optional arguments are set as the uncertainties of e.g. girder offsets in the sigma structure SC.SIG.Support.

INPUT

SC: The SC base structure.
type: String specifying the support structure type. Valid are 'Plinth', 'Girder' or 'Section'.
ords: [2xN] array of ordinates defining start and end locations of N registered support structures.

RETURN VALUE

SC: The base structure containing required information of support structure.

OPTIONS

The following options can be given as name/value-pairs:

'Offset': A [1x3] array defining horizontal, vertical and longitudinal offset uncertainties for the start points or [2x3] array defining horizontal, vertical and longitudinal offset uncertainties for the start end endpoints. If end points have dedicated uncertainties, SCapplyErrors applies random offset errors of both start end endpoints of the corresponding support structure, effectively tilting the support structure. If only start points have asigned uncertainties, SCapplyErrors applies to the support structure endpoints the same offset error as to the start points, resulting in a paraxial translation of the element. Only in this case dedicated 'Roll' uncertainties may be given which then tilt the structure around it’s center. The actual magnet or BPM offsets resulting from the support structure offsets is calculated in SCupdateSupport by interpolating on a straight line between girder start- and endpoints. Note that the coordinate system change due to bending magnets are ignored in this calculation. Thus, the accuracy of the result is limited if dipole magnets are involved. This may be particularly true in case of large sections and/or longitudinal offsets.
'Roll': [1x3] array [az,ax,ay] defining roll (around z-axis), pitch (roll around x-axis) and yaw (roll around y-axis) angle uncertainties.

By default a 2 sigma cutoff is applied. The user can specify a different cutoff by giving the uncertainty as a cell structure, e.g. {[1x3],nSig}, with nSig being the cutoff (see examples below).

EXAMPLES

Registers the girder start end endpoints defined in ords and assigns the horizontal, vertical and longitudinal girder offset uncertainties dX, dY and dZ, respectively, to the girder start points. When the support errors are applied the girder endpoints will get the same offset error as the start points, resulting in a paraxial translation of the girder.

SC = SCregisterSupport(SC,'Girder',ords,'Offset',[dX dY dZ]);

Registers the girder start end endpoints defined in ords and assigns the horizontal, vertical and longitudinal girder offset uncertainties dX, dY and dZ, respectively, to the girder start points with a cutoff value of 3 sigma. When the support errors are applied the girder endpoints will get the same offset error as the start points, resulting in a paraxial translation of the girder.

SC = SCregisterSupport(SC,'Girder',ords,'Offset',{[dX dY dZ],3});

Registers the section start- end endpoints defined in ords and assigns the horizontal and vertical section offset uncertainties dX and dY, respectively, to the start points. When the support errors are applied the section endpoints will get the same offset as the start points.

SC = SCregisterSupport(SC,'Section',ords,'Offset',[dX dY 0]);

Registers the girder start end endpoints defined in ords, assigns the roll uncertainty dPhi and the horizontal and vertical girder offset uncertainties dX1 and dY1, respectively to the start points and dX2 and dY2 to the endpoints. When the support errors are applied, all girder start- and endpoints will get random offset errors and the resulting yaw and pitch angles are calculated accordingly.

SC = SCregisterSupport(SC,'Girder',ords,'Offset',[dX1 dY1 0; dX2 dY2 0],'Roll',[dPhi 0 0]);

Registers the girder start end endpoints defined in ords and assigns the horizontal, vertical and longitudinal girder offset uncertainties dX, dY and dZ, respectively, and the roll, pitch and yaw angle uncertainties az, ax and ay. When the support errors are applied the girders will experience a paraxial translation according to the offsets plus the proper rotations around the three x-, y- and z-axes.

SC = SCregisterSupport(SC,'Girder',ords,'Offset',[dX dY dZ],'Roll',[az ax ay]);

SCsanityCheck

NAME

SCsanityCheck - Checks if the current registration looks reasonable

SYNOPSIS

SCsanityCheck(SC)

DESCRIPTION

Performs a sanity check on the current SC structure adn returns warnings if things look fishy. If you find something that is missing please contact us.

INPUTS

SC: SC base structure

SCscaleCircumference

Name

SCscaleCircumference - scales the circumference of a ring

Synopsis

RING = SCscaleCircumference(RING, circ [, mode])

Description

The circumference of RING is changed by scaling the lengths of the drift spaces in the lattice.

MODE

'abs' (default): The current circumference is scaled to the value circ.
'rel': The current circumference is scaled by the value circ.

Return Value

RING: Lattice with new circumference.

SCsetCMs2SetPoints

NAME

SCsetCMs2SetPoints - Sets dipole corrector magnets to different setpoints

SYNOPSIS

SC = SCsetCMs2SetPoints(SC, CMords, setpoints, nDim [, mode])

DESCRIPTION

Sets horizontal or vertical CMs as specified in CMords and nDim, respectively, to setpoints [rad] and updates the magnetic fields. If the corresponding setpoint exceeds the CM limit specified in the corresponding lattice field CMlimit, the CM is clipped to that value and a warning is being printed (to switch off, use warning('off','SC:CM1')). Positive setpoints will results in kicks in the positive horizontal or vertical direction.

INPUTS

SC: SC base structure
CMords: Array of CM ordinates in the lattice structure
setpoints: CM setpoints (array or single value for all CMs) [rad]
nDim: Integer specifying CM dimension ([1|2] → [hor|ver])

RETURN VALUES

SC: The lattice structure with modified and applied setpoints
setpoints: The list of acutal setpoints applied to the magnets after possible clipping [rad]

MODE

'abs' (default): Use absolute setpoints
'rel': Use setpoints relative to current value
'add': Add setpoints to current value

EXAMPLES

Set all registered horizontal CMs to zero.

SC = SCsetCMs2SetPoints(SC,SC.ORD.CM{1},0,1);

Add 10urad to the fourth registered vertical CM.

SC = SCsetCMs2SetPoints(SC,SC.ORD.CM{2}(4),1E-5, 2,'add');

GLOBALS

isExp: Specify if a real machine is being used, so that a custom user defined function is being called instead

SCsetCavs2SetPoints

NAME

SCsetCavs2SetPoints - Set RF properties to setpoints

SYNOPSIS

SC = SCsetCavs2SetPoints(SC, CAVords, type, setpoints [, mode])

DESCRIPTION

Set the setpoints of Voltage, Frequency or TimeLag as specified in 'type' of the rf cavities specified in CAVords. If only a single setpoint is given for multiple cavities, the setpoint is applied to all cavities.

INPUTS

SC: SC base structure
CAVords: Array of cavity ordinates in the lattice structure
type: String ('Voltage', 'Frequency' or 'TimeLag') specifying which cavity field should be set.
setpoints: Setpoints (array or single value for all cavities)

MODE

'abs' (default): Use absolute setpoint
'rel': Use relative setpoint to current value
'add': Add setpoints to current value

RETURN VALUE

SC: The modified SC structure.

EXAMPLES

Sets the time lag of all cavities registered in SC to zero.

SC = SCsetCavs2SetPoints(SC, SC.ORD.Cavity, 'TimeLag', 0);

Adds 1kHz to the frequency of the first cavity.

SC = SCsetCavs2SetPoints(SC, SC.ORD.Cavity(1), 'Frequency', 1E3, 'add');

% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

SCsetMags2SetPoints

NAME

SCsetMags2SetPoints - Sets magnets to setpoints

SYNOPSIS

SC = SCsetMags2SetPoints(SC, MAGords, type, order, setpoints [, options])

DESCRIPTION

Sets magnets (except CMs) as specified in MAGords to setpoints while order and type defines which field entry should be used (see below). The setpoints may be given relative to their nominal value or in absolute terms. If the considered quadrupole is a combined function magnet with non-zero bending angle and the kick compensation flag is switched on, the appropriate bending angle difference is calculated and the horizontal CM setpoint is changed accordingly to compensate for that dipole kick difference. If the setpoint of a skew quadrupole exceeds the limit specified in the corresponding lattice field SkewQuadLimit, the setpoint is clipped to that value and a warning is being printed (to switch off, use warning('off','SC:SkewLim'))

INPUTS

SC: SC base structure.
MAGords: Magnet ordinates in the lattice structure.
order: Numeric value defining the order of the considered magnet: [1,2,3,…] ⇒ [dip,quad,sext,…]
type: Numeric value defining the type of the considered magnet: [1,2] ⇒ [skew/normal]
setpoints: Magnet setpoints, either single value applied to all magnets or [1 x N] array matching the number of magnets specified in MAGords.

OPTIONS

The following options can be given as name/value-pairs:

'method' ('abs')

Specifies how the setpoints should be applied. Possible are

'abs': Applies the setpoints specified in setpoints.
'rel': Applies the setpoints specified in setpoints relative to the nominal setpoints of the considered magnets.
'add': Adds the setpoints specified in setpoints to the current setpoints of the considered magnets.

'dipCompensation' (0)

Used for combined function magnets. If this flag is set and if there is a horizontal CM registered in the considered magnet, the CM is used to compensate the bending angle difference if the applied quadrupole setpoints differs from the design value.

RETURN VALUES

SC: The base structure containing lattice with modified and applied setpoints.

EXAMPLES

Identify the ordinates of all elements named 'SF' and switch their sextupole component off.

ords = SCgetOrds(SC.RING,'SF');
SC = SCsetMags2SetPoints(SC,ords,2,3,0,'method','abs');

Identify the ordinates of all elements named QF and QD and set their quadrupole component to 99% of their design value.

ords = SCgetOrds(SC.RING,'QF|QD');
SC = SCsetMags2SetPoints(SC,ords,2,2,0.99,'method','rel');

SCsetMultipoles

NAME

SCsetMultipoles - sets multipole errors in lattice elements

SYNOPSIS

RING = SCsetMultipoles(RING, ords, AB [, options])

DESCRIPTION

Applies multipole errors specified in AB in the lattice elements ords of RING depending on the specified options.

INPUTS

RING: Lattice cell structure.
ords: Ordinates of the considered magnets.
AB: [N x 2] array of PolynomA/B multipole errors.

OPTIONS

The following options can be given as name/value-pairs:

'method' ('rnd')

Specifies which multipole error method should be applied. Possible are

'sys': This option is intended for normalized systematic multipole error tables. It sets the systematic multipoles of the field component defined by option 'order' and 'type'. It is required that the AB entries are normalized by that component, e.g. AB(2,1)=1 for skew-quadrupole systematic multipoles. The systematic multipoles are from now on scaled with the current magnet excitation and added to the PolynomA/B fields.
'rnd': This option is intended for random multipole error tables. It randomly generates multipole components with a 2-sigma truncated Gaussian distribution from each of the AB entries. The final multipole errors are stored in the PolynomA/BOffset of the lattice elements.

'order' ([])

Numeric value defining the order of the considered magnet: [1,2,3,…] ⇒ [dip,quad,sext,…]

'type' ([])

Numeric value defining the type of the considered magnet: [1,2] ⇒ [skew/normal]

EXAMPLES

Defines random multipole components for the 'QF' magnet and adds it to the field offsets of all magnets named 'QF'.

ords = SCgetOrds(SC.RING,'QF');
AB = [0 1E-5;...
0 1E-4;...
0 0;...
0 1E-2];
RING = SCsetMultipoles(RING,ords,AB,'method','rnd');

Reads the normalized systematic multipole components for the skew quadrupole excitation of the 'SF' magnet from table 'SF_skew_quad_AT_norm.tsv' and assigns it to all magnets named 'SF'. Note that the data table in 'SF_skew_quad_AT_norm.tsv' must be 1.0 for the skew quadrupole component.

ords = SCgetOrds(SC.RING,'SF');
[AB,order,type] = SCmultipolesRead('SF_skew_quad_AT_norm.tsv');
RING = SCsetMultipoles(RING,ords,AB,'method','sys','order',order,'type',type);

SCsynchEnergyCorrection

NAME

SCsynchEnergyCorrection - Calculates a beam based correction to the rf frequency

SYNOPSIS

[deltaF, ERROR] = SCsynchEnergyCorrection(SC [, options])

DESCRIPTION

Changes the cavity frequency within the user defined interval and evaluates the mean turn-by-turn horizontal BPM deviation. A straight line is fitted to the data and the zero crossing is identified. It is assumed that the beam is injected relatively close to the synchronous phase. Then, for sufficiently small number of turns the synchrotron motion results in a mean turn-by-turn energy deviation which is zero if the synchronous energy defined by the rf frequency matches the injected beam energy. The number of evaluated turns should be smaller than synchrotron period. Note that if more than one cavity is specified the same frequency steps are applied to all cavities. Not also that results might be compromised if the beam transmission differs significantly throughout the different applied frequency steps.

INPUTS

SC: The SC base structure

OPTIONS

The following options can be given as name/value-pairs:

'cavOrd' (SC.ORD.Cavity): Ordinate of evaluated cavity
'range' ([-1E3,1E3]): Frequency range [Hz]
'nSteps' (15): Number of frequency steps to be evaluated
'nTurns' (150): Number of turns to be evaluated
'minTurns' (50): Minimum number of turns the beam has to survive in order to be included in the calculation.
'plotResults' (0): If true, results are plotted.
'plotProgress' (0): If true, each frequency step is plotted.
'verbose' (0): If true, debug information is printed.

RETURN VALUES

deltaF: Frequency correction step to be added to cavity frequency.
ERROR: Error value.

ERRORS

0: All good.
1: Horizontal TBT BPM deviation shows no zero crossing
2: Sinusoidal fit function shows no zero crossing

SCsynchPhaseCorrection

NAME

SCsynchPhaseCorrection - Calculates a beam based correction to the rf cavity phase

SYNOPSIS

[deltaPhi, ERROR] = SCsynchPhaseCorrection(SC [, options])

DESCRIPTION

Changes the cavity phase within the phase interval [-pi,pi] stepwise and evaluates the mean turn-by-turn horizontal BPM deviation. A sinusoidal function is fitted to the data and the zero crossing is identified. It is assumed that for sufficiently small number of turns the synchrotron motion is negligible and injection at the synchronous phase will result in zero turn-by-turn energy variation. Thus, the horizontal turn-by-turn BPM readings should in first approximation not differ. The number of evaluated turns should be significantly smaller than half a sunchrotron period. Note that if more than one cavity is specified the same phase steps are applied to all cavities. Results might be compromised.

INPUTS

SC: The SC base structure

OPTIONS

The following options can be given as name/value-pairs:

'cavOrd' (SC.ORD.Cavity): Ordinate of evaluated cavity
'nSteps' (30): Number of phase steps to be evaluated
'nTurns' (30): Number of turns to be evaluated
'plotResults' (0): If true, results are plotted.
'plotProgress' (0): If true, each phase step is plotted.
'verbose' (0): If true, debug information is printed.

RETURN VALUES

deltaPhi: Phase correction step to be added to cavity field 'TimeLag'.
ERROR: Error value.

ERRORS

0: All good.
1: Horizontal TBT BPM deviation shows no zero crossing
2: Sinusoidal fit function shows no zero crossing

SCtuneScan

NAME

SCtuneScan - Varies quadrupole families to improve beam transmission.

SYNOPSIS

[qSP, SC, maxTurns, finTrans, ERROR] = SCtuneScan(SC, qOrds, qSPvec [, options])

DESCRIPTION

Varies two quadrupole groups specified in cell array qOrds on a grid of relative setpoints specified in qSPvec in a spiral-like pattern to increase the beam transmission. Returns the relative setpoints which satisfied the target condition or, if the target could not be reached the values which resulted in best transmission.

INPUTS

SC: SC base structure
qOrds: [1x2] cell array of quadrupole ordinates {[1 x NQ1],[1 x NQ2]}
qSPvec: [1x2] cell array of quadrupole setpoints {[SP1_1,…,SP1_N1],[SP2_1,…,SP2_N2]} with N2=N1.

OPTIONS

The following options can be given as name/value-pairs:

'nParticles' (SC.INJ.nParticles): Number of particles used for tracking.
'nTurns' (SC.INJ.nTurns): Number of turns used for tracking.
'target' (1): Transmission target at 'nTurns'.
'fullScan' (0): If false, the scan finishes as soon as the target is reached.
'plotFlag' (0): If true, beam transmission is plotted at every step.
'verbose' (0): If true, additional information is printed.

RETURN VALUES

qSP: Final setpoints of quadrupole families (relative to current values)
SC: SC structure with applied setpoints
maxTurns: Array of achieved turns matching the scanning pattern
finTrans: Array of turn-by-turn beam transmission matching the scanning pattern
ERROR: Error value.

ERRORS

0: Beam transmission target reached.
1: Beam transmission or number of turns increased, target not reached.
2: Unable to increase beam transmission.

SCupdateCAVs

NAME

SCupdateCAVs - Updates the cavities in the lattice

SYNOPSIS

SC = SCupdateCAVs(SC [, ords])

DESCRIPTION

Updates the cavity fields Voltage, Frequency and TimeLag in SC.RING as specified in ords. If no ordinates are given explicitly, all registered cavities defined in SC.ORD.Cavity are updated. For each cavity and each field, the setpoints, calibration errors and offsets are considered.

INPUT

SC: Base structure.
ords (optional): Cavity ordinates to be updated.

RETURN VALUE

SC: Base structure with updated cavities.

SCupdateMagnets

NAME

SCupdateMagnets - Updates the magnetic fields in RING

SYNOPSIS

SC = SCupdateMagnets(SC [, ords])

DESCRIPTION

Updates the magnets specified in RING as specified in ords. If no ordinates are given explicitly, all registered magnets defined in SC.ORD.Magnet are updated. For each magnet the setpoints (SetPointA/B) and calibration errors (CalErrorA/B) are evaluated. If systematic multipole components are specified, e.g. in SysPolBFromB for systematic PolynomB-multipoles induced by PolynomB entries, the corresponding multipole components are scaled by the current magnet excitation and added, as well as static field offsets (if specified in PolynomA/BOffset). If the considered magnet has a bending angle error (from pure bending angle eror or due to a combined function magnet), the corresponding horizontal dipole magnetic field is calculated and added to the PolynomB(1) term. It is thereby assured that a dipole error doesn’t alter the coordinate system.

If the considered magnet is registered as a slpit magnet ('MasterOf'), the errors and setpoints of the master magnet are applied to the fields of the child magnets. Note that split quadrupole magnets with different gradients, however, or split CMs can currently not be updated correctly.

RETURN VALUE

SC: Base structure with updated magnets.

SCupdateSupport

NAME

SCupdateSupport - updates the misalignments resulting from the support structure

SYNOPSIS

SC = SCupdateSupport(SC [, options])

DESCRIPTION

This function updates the offsets and rolls of the elements in SC.RING based on the current support errors, by setting the lattice fields T1, T2, and R1, R2 for magnets and the fields SupportOffset and SupportRoll for BPMs.

INPUT

SC: Initial SC base structure.

OPTIONS

The following options can be given as name/value-pairs:

'BPMstructOffset' (1): If true, BPM offsets are updated.
'MAGstructOffset' (1): If true, magnet offsets are updated.
'ords' ([]): List of ordinates at which misalignments should be updated. If empty, all magnets and BPMs are updated.

RETURN VALUE

SC: Base structure with updated SC.RING.

SC Manual

Introduction

Initialization

Error Source Definition & Registration

Generation of a Machine Realization

Interaction with the Machine

Error Sources

BPMs

Cavities

Magnets

Higher order multipoles

Injected beam

Support and Alignment

SC Usage Example - FODO Lattice

Setup enviroment

Define lattice file

Initialize toolbox

Register lattice in SC

Define lattice apertures

Check registration

Apply errors

Setup correction chain

Start correction chain

Perform LOCO based linear optics correction.

Function Categories

Initialization

Tracking

Error Model

Visualization

Correction Scripts

Lattice Properties

Lattice Manipulation

Function List

SCBBA

NAME

SYNOPSIS

DESCRIPTION

INPUTS

RETURN VALUES

OPTIONS

ERROR FLAGS

SEE ALSO

SCapplyErrors

NAME

SYNOPSIS

INPUT

DESCRIPTION

OPTIONS

RETURN VALUE

SEE ALSO

SCcronoff

NAME

SYNOPSIS

DESCRIPTION

RETURN VALUE

EXAMPLES

SCdynamicAperture

NAME

SYNOPSIS

DESCRIPTION

INPUT

OPTIONS

GLOBALS

RETURN VALUES

SCfeedbackBalance

NAME

SYNOPSIS

DESCRIPTION

INPUT

OPTIONS

RETURN VALUES

ERRORS

SEE ALSO

SCfeedbackFirstTurn

NAME

SYNOPSIS

DESCRIPTION

INPUT

OPTIONS

RETURN VALUES